
分析 (1)由根與系數的關系可得出tanA•tanB=12k2-37k+26,根據正切的定義即可得出tanA•tanB=$\frac{a}{b}$•$\frac{b}{a}$=1,由此即可得出關于k的一元二次方程,解之即可得出k的值,將k值代入原方程再根據根的判別式△≥0即可確定k的值;
(2)將k的值代入原方程,解方程求出x的值,分a<b和a>b兩種情況考慮,根據x的值結合c=10利用勾股定理即可求出a、b的值,此題得解.
解答 解:(1)∵tanA、tanB是關于x的一元二次方程x2-kx+12k2-37k+26=0的兩個實數根,
∴tanA•tanB=12k2-37k+26.
又∵tanA•tanB=$\frac{a}{b}$•$\frac{b}{a}$=1,
∴12k2-37k+26=1,
解得:k1=$\frac{25}{12}$,k2=1.
當k2=1時,原方程化為x2-x+1=0,
此時△=(-1)2-4×1×1<0,不合題意,舍去,
∴k=$\frac{25}{12}$.
(2)當k=$\frac{25}{12}$時,原方程化為x2-$\frac{25}{12}$x+1=0,
解得:x1=$\frac{4}{3}$,x2=$\frac{3}{4}$.
①當a>b時,∴tanA=$\frac{a}{b}$=$\frac{4}{3}$,
不妨設a=4m,b=3m(m>0),
∴c=5m,
∵c=10,
∴5m=10,
∴m=2,
∴a=8,b=6;
②當a<b時,∴tanA=$\frac{a}{b}$=$\frac{3}{4}$,
同理可得a=6,b=8.
∴a=6,b=8或a=8,b=6.
點評 本題考查了根的判別式、根與系數的關系以及勾股定理,利用勾股定理求出三角形的兩直角邊長是解題的關鍵.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:初中數學 來源: 題型:解答題
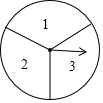 如圖,一個轉盤被分成3等分,每一份上各寫有一個數字,隨機轉動轉盤2次,第一次轉到的數字數字為十位數字,第二次轉到的數字為個位數字,2次轉動后組成一個兩位數(若指針停在等分線上則重新轉一次)
如圖,一個轉盤被分成3等分,每一份上各寫有一個數字,隨機轉動轉盤2次,第一次轉到的數字數字為十位數字,第二次轉到的數字為個位數字,2次轉動后組成一個兩位數(若指針停在等分線上則重新轉一次)查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com