
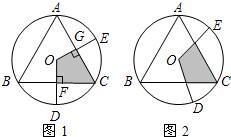
證明:(1)如圖1,連接OA,OC;
因為點O是等邊三角形ABC的外心,
所以Rt△OFC≌Rt△OGC≌Rt△OGA,
S
四邊形OFCG=2S
△OFC=S
△OAC,
因為S
△OAC=

S
△ABC,
所以S
四邊形OFCG=

S
△ABC.
(2)證法一:
連接OA,OB和OC,則
△AOC≌△COB≌△BOA,∠1=∠2;
設(shè)OD交BC于點F,OE交AC于點G,

∠AOC=∠3+∠4=120°,∠DOE=∠5+∠4=120°,
∴∠3=∠5;
在△OAG和△OCF中

,
∴△OAG≌△OCF,
∴S
△OAG=S
△OCF,
∴S
△OAG+S
△OGC=S
△OCF+S
△OGC,
即S
四邊形OFCG=S
△OAC=

S
△ABC;
證法二:
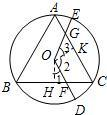
設(shè)OD交BC于點F,OE交AC于點G;
作OH⊥BC,OK⊥AC,垂足分別為H、K;
在四邊形HOKC中,∠OHC=∠OKC=90°,∠C=60°,
∴∠HOK=360°-90°-90°-60°=120°,
即∠1+∠2=120度;
又∵∠GOF=∠2+∠3=120°,
∴∠1=∠3,
∵AC=BC,
∴OH=OK,
∴△OGK≌△OFH,
∴S
四邊形OFCG=S
四邊形OHCK=

S
△ABC.
分析:(1)本題要依靠輔助線的幫助.連接OA,OC,證明Rt△OFC≌Rt△OGC≌Rt△OGA后求得S
△OAC=

S
△ABC,易證S
OFCG=

S
△ABC.
(2)本題有多種解法.連接OA,OB和OC,證明△AOC≌△COB≌△BOA,求出∠AOC以及∠DOE之間的關(guān)系即可.
點評:本題涉及三角形的外接圓知識及全等三角形的判定,難度偏難.

 .
. 中陰影部分)面積始終是△ABC的面積的
中陰影部分)面積始終是△ABC的面積的 .
. 證明:(1)如圖1,連接OA,OC;
證明:(1)如圖1,連接OA,OC; S△ABC,
S△ABC, S△ABC.
S△ABC.
 ,
, S△ABC;
S△ABC; 設(shè)OD交BC于點F,OE交AC于點G;
設(shè)OD交BC于點F,OE交AC于點G; S△ABC.
S△ABC. S△ABC,易證SOFCG=
S△ABC,易證SOFCG= S△ABC.
S△ABC.

 智趣寒假作業(yè)云南科技出版社系列答案
智趣寒假作業(yè)云南科技出版社系列答案 中陰影部分)面積始終是△ABC的面積的
中陰影部分)面積始終是△ABC的面積的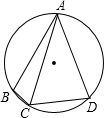 如圖:在圓內(nèi)接四邊形ABCD中,AB=AD,AC=1,∠ACD=60°,則四邊ABCD的面積為( )
如圖:在圓內(nèi)接四邊形ABCD中,AB=AD,AC=1,∠ACD=60°,則四邊ABCD的面積為( )