
分析 (1)根據關于x的方程x2-(m+2)x+m+1=0判別式的符號進行證明;
(2)將已知函數解析式轉化為兩點式方程,求得點A、B的橫坐標,然后結合已知條件求得m的值即可;
(3)根據題意作出圖形,結合圖形直接寫出n的取值范圍.
解答 解:(1)∵△=(m+2)2-4(m+1)=m2≥0,
∴不論m取何值,該方程總有實數根;
(2)由題意可知:y=x2-(m+2)x+m+1=(x-1)(x-m-1),
∴A(1,0),B(m+1,0).
∵兩交點間距離為2,
∴m+1-1=2.
∴m=2.
∴y=x2-4x+3;
(3)如圖所示,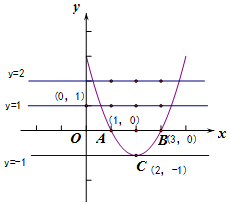
n的取值范圍是:1≤n<2.
點評 本題考查了二次函數綜合題,需要掌握拋物線與x軸的交點、拋物線解析式的三種形式間的轉化、拋物線解析式與一元二次方程的轉化等知識,解題的關鍵是靈活運用這些知識解決問題,屬于中考常考題型.


科目:初中數學 來源: 題型:填空題
| 應聘者 | 語言 | 商品知識 |
| 甲 | 70 | 80 |
| 乙 | 80 | 70 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知AC是矩形ABCD的對角線,過AC的中點O的直線EF,交BC于點F,交BC于點F,交AD于點E,連接AF,CE.
如圖,已知AC是矩形ABCD的對角線,過AC的中點O的直線EF,交BC于點F,交BC于點F,交AD于點E,連接AF,CE.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
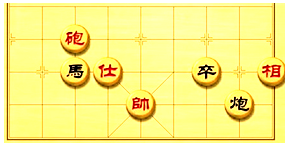 象棋在中國有著三千多年的歷史,屬于二人對抗性游戲的一種.由于用具簡單,趣味性強,成為流行極為廣泛的棋藝活動.如圖是一方的棋盤,如果“馬”的坐標是(-2,2),它是拋物線y=ax2(a≠0)上的一個點,那么下面哪個棋子在該拋物線上( )
象棋在中國有著三千多年的歷史,屬于二人對抗性游戲的一種.由于用具簡單,趣味性強,成為流行極為廣泛的棋藝活動.如圖是一方的棋盤,如果“馬”的坐標是(-2,2),它是拋物線y=ax2(a≠0)上的一個點,那么下面哪個棋子在該拋物線上( )| A. | 帥 | B. | 卒 | C. | 炮 | D. | 仕 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 已知圖中的每個小正方格都是邊長為1的小正方形,若△ABC與△A1B1C1是位似圖形,且頂點都在小正方形頂點上,則它們的位似中心的坐標是(9,0).
已知圖中的每個小正方格都是邊長為1的小正方形,若△ABC與△A1B1C1是位似圖形,且頂點都在小正方形頂點上,則它們的位似中心的坐標是(9,0).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com