
【題目】已知:如圖,∠A+∠D=180°,∠1=3∠2,∠2=24°,點P是BC上的一點.
(1)請寫出圖中∠1的一對同位角,一對內錯角,一對同旁內角;
(2)求∠EFC與∠E的度數;
(3)若∠BFP=46°,請判斷CE與PF是否平行?

【答案】(1)見解析;(2)∠EFC=108°;(3)不平行,理由見解析.
【解析】
(1)根據同位角、內錯角以及同旁內角的定義,即可得出結論;
(2)由∠A+∠D=180°可得出AB∥CD,根據平行線的性質可得出∠1=∠DFE,再結合∠1=3∠2、∠2=24°通過角的計算即可得出∠EFC與∠E的度數;
(3)由(2)中∠E的度數結合∠BFP=46°,即可得出∠E≠∠BFP,從而得出CE與PF不平行.
(1)同位角:∠1與∠DFE;內錯角:∠1與∠BFC;同旁內角:∠1與∠DFB.
(2)∵∠A+∠D=180°,
∴AB∥CD,
∴∠1=∠DFE.
∵∠1=3∠2,∠2=24°,
∴∠1=∠DFE=72°.
∵∠DFE=∠E+∠2,
∴∠E=48°.
∵∠DFE=180°-∠EFC,
∴∠EFC=108°.
(3)不平行.
∵∠E=48°,∠BFP=46°,
∴∠E≠∠BFP,
∴CE與PF不平行.


 黃岡冠軍課課練系列答案
黃岡冠軍課課練系列答案科目:初中數學 來源: 題型:
【題目】如圖①,平面直角坐標系中,O為原點,點A坐標為(﹣4,0),AB∥y軸,點C在y軸上,一次函數y=![]() x+3的圖象經過點B、C.
x+3的圖象經過點B、C.

(1)點C的坐標為_____,點B的坐標為_____;
(2)如圖②,直線l經過點C,且與直線AB交于點M,O'與O關于直線l對稱,連接CO'并延長,交射線AB于點D.
①求證:△CMD是等腰三角形;
②當CD=5時,求直線l的函數表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在數軸上點A表示數a,點B表示數b,點C表示數c,b是最小的正整數,且a,c滿足|a+2|+(c-7)2=0.
(1)填空:a=________,b=________,c=________;
(2)畫出數軸,并把A,B,C三點表示在數軸上;
(3)P是數軸上任意一點,點P表示的數是x,當PA+PB+PC=10時,x的值為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
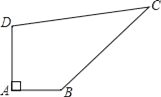
【題目】已知某開發區有一塊四邊形的空地ABCD,如圖所示,現計劃在空地上種植草皮,經測量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,問要多少投入?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在數軸上有A、B、C、D四個點,且線段AB=4,CD=6,已知A表示的數是﹣10,C表示的數是8,若線段AB以每秒6個單位長度的速度,線段CD以每秒2個單位長度的速度在數軸上運動(A在B左側,C在D左側)
(1)B,D兩點所表示的數分別是 、 ;
(2)若線段AB向右運動,同時線段CD向左運動,經過多少秒時,BC=2;
(3)若線段AB、CD同時向右運動,同時點P從原點出發以每秒1個單位長度的速度向右運動,經過多少秒時,點P到點A,C的距離相等?
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列圖形,第一個圖2條直線相交最多有1個交點,第二個圖3條直線相交最多有3個交點,第三個圖4條直線相交最多有6個交點,…,像這樣,則20條直線相交最多交點的個數是( )
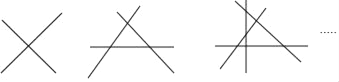
A. 171 B. 190 C. 210 D. 380
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知線段AB,按下列要求完成畫圖和計算:
(1)延長線段AB到點C,使BC=2AB,取AC中點D;
(2)在(1)的條件下,如果AB=4,求線段BD的長度.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中學生騎電動車上學給交通安全帶來隱患,為了解某中學2 500個學生家長對“中學生騎電動車上學”的態度,從中隨機調查400個家長,結果有360個家長持反對態度,則下列說法正確的是( )
A. 調查方式是普查 B. 該校只有360個家長持反對態度
C. 樣本是360個家長 D. 該校約有90%的家長持反對態度
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com