
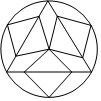
 如圖,由等邊三角形、正方形、圓組成的軸對稱圖案中,等邊三角形與正方形的邊長的比值為( )
如圖,由等邊三角形、正方形、圓組成的軸對稱圖案中,等邊三角形與正方形的邊長的比值為( )| A. | $\frac{{\sqrt{6}}}{2}$ | B. | 3 | C. | $\sqrt{6}$ | D. | $\frac{{3\sqrt{3}}}{2}$ |
分析 由題意知:三個正方形的共用頂點即為圓的圓心,也是等邊三角形的重心;可設等邊三角形的邊長為2x,作等邊三角形,再根據三角形重心的性質即可得到正方形的對角線的長,求出正方形的邊長,即可得出答案.
解答 解:如圖,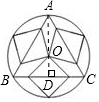
設圓的圓心為O,由題意知:三角形的重心以及三個正方形的共用頂點即為點O.
過A作AD⊥BC于D,則AD必過點O,且AO=2OD;
設△ABC的邊長為2x,則BD=x,AD=$\sqrt{(2x)^{2}-{x}^{2}}$=$\sqrt{3}$x,
OD=$\frac{\sqrt{3}}{3}$x;
∴正方形的邊長為:$\frac{\sqrt{6}}{3}$x,
∴等邊三角形與正方形的邊長的比值是2x:$\frac{\sqrt{6}}{3}$x=$\sqrt{6}$,
故選C.
點評 此題考查的知識點有:軸對稱圖形、等邊三角形及正方形的性質、三角形重心的性質等知識點,找到等邊三角形和正方形邊長的比例關系是解答此題的關鍵.


 名師點撥卷系列答案
名師點撥卷系列答案 英才計劃期末調研系列答案
英才計劃期末調研系列答案科目:初中數學 來源: 題型:選擇題
| A. | m>0 | B. | m<0 | C. | m>1 | D. | m<1 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{3}{5}$ | B. | $\frac{5}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | a、b、c都是奇數 | |
| B. | a、b、c或都是奇數或至少有兩個偶數 | |
| C. | a、b、c都是偶數 | |
| D. | a、b、c中至少有兩個偶數 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 三角形的中線、角平分線,高線都是線段 | |
| B. | 有一個內角是直角的三角形是直角三角形 | |
| C. | 任意三角形的外角和都是360° | |
| D. | 三角形的一個外角大于任何一個內角 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | m=4,n=12 | B. | m=-4,n=12 | C. | m=-4,n=-12 | D. | m=4,n=-12 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com