解答:
(1)解:由題意把A(-3,0)、B(0,3)、C(1,0)代入y=ax
2+bx+c列方程組得:
,解得
.
∴拋物線的解析式是y=-x
2-2x+3.
∵y=-x
2-2x+3=-(x+1)
2+4,
∴拋物線的頂點D的坐標為(-1,4).
(2)存在.
理由:方法(一):
由旋轉得∠EDF=60°,在Rt△DEF中,∵∠EDF=60°,DE=4,
∴EF=DE×tan60°=4
.∴OF=OE+EF=1+4
.
∴F點的坐標為(
-1-4,0).
設過點D、F的直線解析式是y=κx+b,
把D(-1,4),F(
-1-4,0)
代入求得
y=x+4+.
分兩種情況:①當點M在射線ND上時,
∵∠MON=75°,∠BON=45°,
∴∠MOB=∠MON-∠BON=30°.∴∠MOC=60°.
∴直線OM的解析式為y=
x.
∴點M的坐標為方程組.
的解,解方程組得,
.
∴點M的坐標為(
2+,
6+).
②當點M在射線NF上時,不存在點M使得∠MON=75°
理由:∵∠MON=75°,∠FON=45°,∴∠FOM=∠MON-∠FON=30°.
∵∠DFE=30°,∴∠FOM=∠DFE.∴OM∥FN.∴不存在,
綜上所述,存在點M,且點M的坐標為(
2+,
6+).
方法(二)①M在射線ND上,過點M作MP⊥x軸于點P,
由旋轉得∠EDF=60°,在Rt△DEF中,∵∠EDF=60°,DE=4
∴EF=DE×tan60°=4
.∴OF=OE﹢EF=1+4
.
∵∠MON=75°,∠BON=45°,∴∠MOB=∠MON-∠BON=30°.
∴∠MOC=60°.在Rt△MOP中,∴MP=
OP.
在Rt△MPF中,∵tan∠MFP=
,
∴
=
.
∴OP=2
﹢
.∴MP=6﹢
.
∴M點坐標為(2
﹢
、6﹢
),
②M在射線NF上,不存在點M使得∠MON=75°
理由:∵∠MON=75°,∠FON=45°,∴∠FOM=∠MON-∠FON=30°.
∵∠DFE=30°.∴∠FOM=∠DFE.∴OM∥DN.∴不存在.
綜上所述,存在點M,且點M的坐標為(
2+,
6+).
(3)有兩種情況①直角梯形OBPQ中,PQ∥OB,∠OBP=90°.
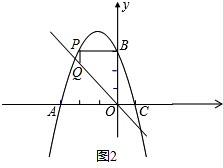
如圖2,∵∠OBP=∠AOB=90°,∴PB∥OA.
所以點P、B的縱坐標相同都是3.
因為點P在拋物線y=-x
2-2x+3上,
把y=3代入拋物線的解析式中得x
1=0(舍去),x
2=-2.
由PQ∥OB得到點P、Q的橫坐標相同,
都等于-2.把x=-2代入y=-x得y=2.
所以Q點的坐標為(-2,2).
②在直角梯形OBPQ中,PB∥OQ,∠BPQ=90°.
如圖3,∵D(-1,4),B(0,3),∴DB∥OQ.∵PB∥OQ,
點P在拋物線上,∴點P、D重合.
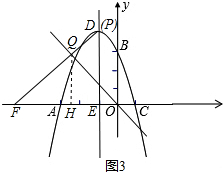
∴∠EDF=∠EFD=45°.∴EF=ED=4.
∴OF=OE+EF=5.
作QH⊥x軸于H,∵∠QOF=∠QFO=45°,
∴OQ=FQ.∴OH=
OF=
.
∴Q點的橫坐標-
.∵Q點在y=-x上,∴把x=-
代入y=-x得y=
.∴Q點的坐標為(-
,
).
綜上,符合條件的點Q有兩個,坐標分別為:(-2,2),(-
,
).


 (1)解:由題意把A(-3,0)、B(0,3)、C(1,0)代入y=ax2+bx+c列方程組得:
(1)解:由題意把A(-3,0)、B(0,3)、C(1,0)代入y=ax2+bx+c列方程組得:
 ∴∠EDF=∠EFD=45°.∴EF=ED=4.
∴∠EDF=∠EFD=45°.∴EF=ED=4.

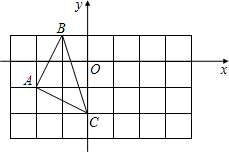 (2012•營口)如圖,在平面直角坐標系中,△ABC的三個頂點坐標分別為A(-2,-1)、B(-1,1)、C(0,-2).
(2012•營口)如圖,在平面直角坐標系中,△ABC的三個頂點坐標分別為A(-2,-1)、B(-1,1)、C(0,-2). (2012•營口一模)[提出問題]:已知矩形的面積為1,當該矩形的長為多少時,它的周長最小?最小值是多少?
(2012•營口一模)[提出問題]:已知矩形的面積為1,當該矩形的長為多少時,它的周長最小?最小值是多少?