
【題目】閱讀材料:
我們知道![]() 的幾何意義是在數(shù)軸上數(shù)
的幾何意義是在數(shù)軸上數(shù)![]() 對應(yīng)的點與原點的距離,即
對應(yīng)的點與原點的距離,即![]() ,也就是說
,也就是說![]() 表示在數(shù)軸上數(shù)
表示在數(shù)軸上數(shù)![]() 與數(shù)
與數(shù)![]() 對應(yīng)的點之間的距離,這個結(jié)論可以推廣為
對應(yīng)的點之間的距離,這個結(jié)論可以推廣為![]() 表示數(shù)軸上
表示數(shù)軸上![]() 與
與![]() 對應(yīng)點之間的距離.
對應(yīng)點之間的距離.
例1:已知![]() ,求
,求![]() 的值.
的值.
解:容易看出,在數(shù)軸上與原點距離為![]() 的點的對應(yīng)數(shù)為
的點的對應(yīng)數(shù)為![]() 和
和![]() ,即
,即![]() 的值為
的值為![]() 和
和![]() .
.
例2:已知![]() ,求
,求![]() 的值.
的值.
解:在數(shù)軸上與![]() 的距離為
的距離為![]() 的點的對應(yīng)數(shù)為
的點的對應(yīng)數(shù)為![]() 和
和![]() ,即
,即![]() 的值為
的值為![]() 和
和![]() .
.
仿照閱讀材料的解法,求下列各式中的值.
(1)![]()
(2)![]()
(3)由以上探索猜想:對于任何有理數(shù)![]() 是否有最小值?如果有,寫出最小值;如果沒有,請說明理由.
是否有最小值?如果有,寫出最小值;如果沒有,請說明理由.
【答案】(1)-3和3;(2)-6和2;(3)有最小值,最小值為3
【解析】
(1)由閱讀材料中的方法求出![]() 的值即可;
的值即可;
(2)由閱讀材料中的方法求出![]() 的值即可;
的值即可;
(3)根據(jù)題意得出原式最小時![]() 的范圍,并求出最小值即可.
的范圍,并求出最小值即可.
(1)![]() ,在數(shù)軸上與原點距離為3的點的對應(yīng)數(shù)為-3和3,即
,在數(shù)軸上與原點距離為3的點的對應(yīng)數(shù)為-3和3,即![]() 的值為-3和3;
的值為-3和3;
(2)![]() ,在數(shù)軸上與-2距離為4的點的對應(yīng)數(shù)為-6和2,即
,在數(shù)軸上與-2距離為4的點的對應(yīng)數(shù)為-6和2,即![]() 的值為-6和2;
的值為-6和2;
(3)有最小值,最小值為3,
理由是:
∵![]() 理解為:在數(shù)軸上表示
理解為:在數(shù)軸上表示![]() 到3和6的距離之和,
到3和6的距離之和,
∴當(dāng)![]() 在3與6之間的線段上(即
在3與6之間的線段上(即![]() )時:
)時:
即![]() 的值有最小值,最小值為
的值有最小值,最小值為![]() .
.


 學(xué)練快車道快樂假期寒假作業(yè)系列答案
學(xué)練快車道快樂假期寒假作業(yè)系列答案 新思維寒假作業(yè)系列答案
新思維寒假作業(yè)系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】觀察下面三行單項式:
![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…;①
,…;①
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…;②
,…;②
![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() ,…;③
,…;③
根據(jù)你發(fā)現(xiàn)的規(guī)律,解答下列問題:
(1)第①行的第8個單項式為 ;
(2)第②行的第9個單項式為 ;
(3)第③行的第n個單項式為 (用含n的式子表示);
(4)取每行的第8個單項式,令這三個單項式的和為A.
當(dāng)![]() 時,求A的值.
時,求A的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】兒童節(jié)期間,某公園游戲場舉行一場活動.有一種游戲的規(guī)則是:在一個裝有8個紅球和若干白球(每個球除顏色外,其他都相同)的袋中,隨機(jī)摸一個球,摸到一個紅球就得到一個海寶玩具.已知參加這種游戲的兒童有40 000人,公園游戲場發(fā)放海寶玩具8 000個.
(1)求參加此次活動得到海寶玩具的頻率?
(2)請你估計袋中白球的數(shù)量接近多少個?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,A(﹣2,0),B(0,4),以B點為直角頂點在第二象限作等腰直角△ABC.
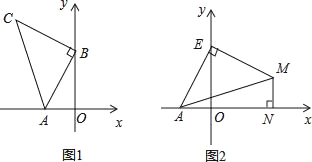
(1)求C點的坐標(biāo);
(2)在坐標(biāo)平面內(nèi)是否存在一點P,使△PAB與△ABC全等?若存在,求出P點坐標(biāo),若不存在,請說明理由;
(3)如圖2,點E為y軸正半軸上一動點,以E為直角頂點作等腰直角△AEM,過M作MN⊥x軸于N,求OE﹣MN的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】求兩個正整數(shù)的最大公約數(shù)是常見的數(shù)學(xué)問題,中國古代數(shù)學(xué)專著《九章算術(shù)》中便記載了求兩個正整數(shù)最大公約數(shù)的一種方法﹣﹣更相減損術(shù),術(shù)曰:“可半者半之,不可半者,副置分母、子之?dāng)?shù),以少成多,更相減損,求其等也.以等數(shù)約之”,意思是說,要求兩個正整數(shù)的最大公約數(shù),先用較大的數(shù)減去較小的數(shù),得到差,然后用減數(shù)與差中的較大數(shù)減去較小數(shù),以此類推,當(dāng)減數(shù)與差相等時,此時的差(或減數(shù))即為這兩個正整數(shù)的最大公約數(shù).
例如:求91與56的最大公約數(shù)
解:
請用以上方法解決下列問題:
(1)求108與45的最大公約數(shù);
(2)求三個數(shù)78、104、143的最大公約數(shù).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,△ABC中,點O是邊AC上一個動點,過O作直線MN∥BC.設(shè)MN交∠ACB的平分線于點E,交∠ACB的外角平分線于點F.

(1)求證:OE=OF;
(2)若CE=12,CF=5,求OC的長;
(3)當(dāng)點O在邊AC上運(yùn)動到什么位置時,四邊形AECF是矩形?并說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,公共汽車行駛在筆直的公路上,這條路上有![]() 四個站點,每相鄰兩站之間的距離為
四個站點,每相鄰兩站之間的距離為![]() 千米,從
千米,從![]() 站開往
站開往![]() 站的車稱為上行車,從
站的車稱為上行車,從![]() 站開往
站開往![]() 站的車稱為下行車.第一班上行車、下行車分別從
站的車稱為下行車.第一班上行車、下行車分別從![]() 站、
站、![]() 站同時發(fā)車,相向而行,且以后上行車、下行車每隔
站同時發(fā)車,相向而行,且以后上行車、下行車每隔![]() 分鐘分別在
分鐘分別在![]() 站同時發(fā)一班車,乘客只能到站點上、下車(上、下車的時間忽略不計),上行車、 下行車的速度均為
站同時發(fā)一班車,乘客只能到站點上、下車(上、下車的時間忽略不計),上行車、 下行車的速度均為![]() 千米/小時.
千米/小時.
![]() 第一班上行車到
第一班上行車到![]() 站、第一班下行車到
站、第一班下行車到![]() 站分別用時多少?
站分別用時多少?
![]() 第一班上行車與第一班下行車發(fā)車后多少小時相距
第一班上行車與第一班下行車發(fā)車后多少小時相距![]() 千米?
千米?
![]() 一乘客在
一乘客在![]() 兩站之間的
兩站之間的![]() 處,剛好遇到上行車,
處,剛好遇到上行車,![]() 千米,他從
千米,他從![]() 處以
處以![]() 千米/小時的速度步行到
千米/小時的速度步行到![]() 站乘下行車前往
站乘下行車前往![]() 站辦事.
站辦事.

①若![]() 千米,乘客從
千米,乘客從![]() 處到達(dá)
處到達(dá)![]() 站的時間最少要幾分鐘?
站的時間最少要幾分鐘?
②若![]() 千米,乘客從
千米,乘客從![]() 處到達(dá)
處到達(dá)![]() 站的時間最少要幾分鐘?
站的時間最少要幾分鐘?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,線段AB、CD相交于點O,連結(jié)AD、CB,我們把形如圖1的圖形稱之為“8字形”.如圖2,在圖1的條件下,∠DAB和∠BCD的平分線AP和CP相交于點P,并且與CD、AB分別相交于點M、N.試解答下列問題:
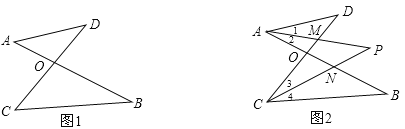
(1)在圖1中,請直接寫出∠A、∠B、∠C、∠D之間的數(shù)量關(guān)系;
(2)仔細(xì)觀察,在圖2中“8字形”有多少個;
(3)圖2中,當(dāng)∠D=50°,∠B=40°時,求∠P的度數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】“十房”天然氣正在緊張施工中,從2018年1月1日起居民生活用氣階梯價格制度將正式實施,一般生活用氣收費(fèi)標(biāo)準(zhǔn)如下表所示,比如6口以下的戶年天然氣用量在第二檔時,其中350立方米按2.28元/m3收費(fèi),超過350立方米的部分按2.5元/m3收費(fèi).小冬一家有五口人,他想幫父母計算一下實行階梯價后,家里天然氣費(fèi)的支出情況.

(1)如果他家2018年全年使用300立方米天然氣,那么需要交多少元天然氣費(fèi)?
(2)如果他家2018年全年使用500立方米天然氣,那么需要交多少元天然氣費(fèi)?
(3)如果他家2018年需要交1563元天然氣費(fèi),他家2018年用了多少立方米天然氣?
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com