
【題目】如圖,若![]() ,添加一個條件使
,添加一個條件使![]() ,則添加的條件是________.
,則添加的條件是________.
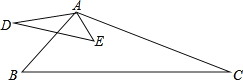
【答案】![]() 或者∠DAB=∠CAE,∠DAE=∠BAC.
或者∠DAB=∠CAE,∠DAE=∠BAC.
【解析】
由已知及相似三角形的判定可以從邊和角兩方面考慮解答.(1)由邊解答,已知兩組對應邊成比例,只要添加第三組對應邊成比例即可.(2)由角解答,只要添加已知兩組對應邊的夾角∠DAB和∠BAC相等即可,又由∠DAB=∠CAE也能推出∠DAB和∠BAC相等即△ADE∽△ACB.
由已知,
若![]() ,則△ADE∽△ACB.
,則△ADE∽△ACB.
若![]() ,∠DAE=∠BAC,則△ADE∽△ACB.
,∠DAE=∠BAC,則△ADE∽△ACB.
若∠DAB=∠CAE,則∠DAB+∠BAE=∠CAE+∠BAE,即,∠DAE=∠BAC,又![]() ,則△ADE∽△ACB.
,則△ADE∽△ACB.
故答案為:![]() 或者∠DAB=∠CAE,∠DAE=∠BAC.
或者∠DAB=∠CAE,∠DAE=∠BAC.


科目:初中數學 來源: 題型:
【題目】如圖,在由邊長為1個單位長度的小正方形組成的10×10網格中,已知點O,A,B均為網格線的交點.
(1)在給定的網格中,以點O為位似中心,將線段AB放大為原來的2倍,得到線段![]() (點A,B的對應點分別為
(點A,B的對應點分別為![]() ).畫出線段
).畫出線段![]() ;
;
(2)將線段![]() 繞點
繞點![]() 逆時針旋轉90°得到線段
逆時針旋轉90°得到線段![]() .畫出線段
.畫出線段![]() ;
;
(3)以![]() 為頂點的四邊形
為頂點的四邊形![]() 的面積是 個平方單位.
的面積是 個平方單位.

查看答案和解析>>
科目:初中數學 來源: 題型:
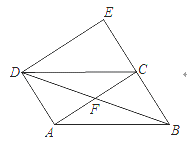
【題目】如圖,ABCD中,點E在BC延長線上,EC=BC,連接DE,AC,AC⊥AD于點A、
(1)求證:四邊形ACED是矩形;
(2)連接BD,交AC于點F.若AC=2AD,猜想∠E與∠BDE的數量關系,并證明你的猜想.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】陽光市場某個體商戶購進某種電子產品,每個進價50元.調查發現,當售價為80元時,平均一周可賣出160個,而當每售價每降低2元時,平均一周可多賣出20個.若設每個電子產品降價x元,
(1)根據題意,填表:
進價(元) | 售價(元) | 每件利潤(元) | 銷量(個) | 總利潤(元) | |
降價前 | 50 | 80 | 30 | 160 |
|
降價后 | 50 | ________ | ________ | ________ | ________ |
(2)若商戶計劃每周盈利5200元,且盡量減少庫存,則每個電子產品應降價多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
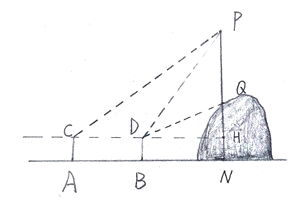
【題目】小明學校門前有座山,山上有一電線桿PQ,他很想知道電線桿PQ 的高度.于是,有一天,小明和他的同學小亮帶著側傾器和皮尺來到山腳下進行測量.測量方案如下:如圖,首先,小明站在地面上的點A處,測得電線桿頂端點P的仰角是45![]() ;然后小明向前走6米到達點B處,測得電線桿頂端點P和電線桿底端點Q的仰角分別是60
;然后小明向前走6米到達點B處,測得電線桿頂端點P和電線桿底端點Q的仰角分別是60![]() 和30
和30![]() ,設小明的眼睛到地面的距離為1.6米.請根據以上測量的數據,計算電線桿PQ的高度(結果精確到1米)參考數據:
,設小明的眼睛到地面的距離為1.6米.請根據以上測量的數據,計算電線桿PQ的高度(結果精確到1米)參考數據:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,AC=BC=6.點P在邊AC上運動,過點P作PD⊥AB于點D,以AP、AD為鄰邊作PADE.設□PADE與△ABC重疊部分圖形的面積為y,線段AP的長為x(0<x≤6).
(1)求線段PE的長(用含x的代數式表示).
(2)當點E落在邊BC上時,求x的值.
(3)求y與x之間的函數關系式.
(4)直接寫出點E到△ABC任意兩邊所在直線距離相等時x的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,PD切⊙O于點C,與BA的延長線交于點D,DE⊥PO交PO延長線于點E,連接PB,∠EDB=∠EPB.
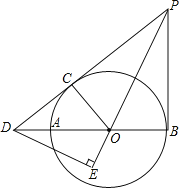
(1)求證:PB是的切線.
(2)若PB=6,DB=8,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,AB=AC,BC交⊙O于點D, AC交⊙O于點E,∠BAC=45°。
(1)求∠EBC的度數;
(2)求證:BD=CD。

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com