
【題目】如圖,在平面直角坐標系![]() 中,拋物線
中,拋物線![]() 與
與![]() 軸交于
軸交于![]() ,
,![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左側),經過點
的左側),經過點![]() 的直線
的直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與拋物線的另一個交點為
,與拋物線的另一個交點為![]() ,且
,且![]() .
.
![]() 直接寫出點
直接寫出點![]() 的坐標,并求直線
的坐標,并求直線![]() 的函數表達式(其中
的函數表達式(其中![]() ,
,![]() 用含
用含![]() 的式子表示);
的式子表示);
![]() 點
點![]() 是直線
是直線![]() 上方的拋物線上的一點,若
上方的拋物線上的一點,若![]() 的面積的最大值為
的面積的最大值為![]() ,求
,求![]() 的值;
的值;
![]() 設
設![]() 是拋物線對稱軸上的一點,點
是拋物線對稱軸上的一點,點![]() 在拋物線上,以點
在拋物線上,以點![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形能否成為矩形?若能,求出點
為頂點的四邊形能否成為矩形?若能,求出點![]() 的坐標;若不能,請說明理由.
的坐標;若不能,請說明理由.
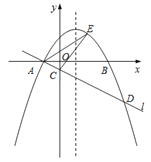
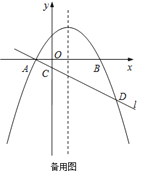
【答案】(1)A(﹣1,0),![]() ;(2)a=﹣
;(2)a=﹣![]() ;(3)
;(3)![]() 點的坐標為
點的坐標為![]() ,
,![]() .
.
【解析】
(1)解方程即可得到結論;根據直線l:y=kx+b過A(﹣1,0),得到直線l:y=kx+k,解方程得到點D的橫坐標為4,求得k=a,得到直線l的函數表達式為y=ax+a;
(2)過E作EF∥y軸交直線l于F,設E(x,ax2﹣2ax﹣3a),得到F(x,ax+a),求出EF=ax2﹣3ax﹣4a,根據三角形的面積公式列方程即可得到結論;
(3)令ax2﹣2ax﹣3a=ax+a,即ax2﹣3ax﹣4a=0,得到D(4,5a),設P(1,m),①若AD是矩形ADPQ的一條邊,②若AD是矩形APDQ的對角線,列方程即可得到結論.
(1)當y=0時,ax2﹣2ax﹣3a=0,解得:x1=﹣1,x2=3,∴A(﹣1,0),B(3,0).
∵直線l:y=kx+b過A(﹣1,0),∴0=﹣k+b,即k=b,∴直線l:y=kx+k.
∵拋物線與直線l交于點A,D,∴ax2﹣2ax﹣3a=kx+k,即ax2﹣(2a+k)x﹣3a﹣k=0.
∵CD=4AC,∴點D的橫坐標為4,∴﹣3﹣![]() =﹣1×4,∴k=a,∴直線l的函數表達式為y=ax+a;
=﹣1×4,∴k=a,∴直線l的函數表達式為y=ax+a;
(2)過E作EF∥y軸交直線l于F,設E(x,ax2﹣2ax﹣3a),則F(x,ax+a),EF=ax2﹣2ax﹣3a﹣ax﹣a=ax2﹣3ax﹣4a,∴S△ACE=S△AFE﹣S△CEF=![]() (ax2﹣3ax﹣4a)(x+1)﹣
(ax2﹣3ax﹣4a)(x+1)﹣![]() (ax2﹣3ax﹣4a)x=
(ax2﹣3ax﹣4a)x=![]() (ax2﹣3ax﹣4a)=
(ax2﹣3ax﹣4a)=![]() a(x﹣
a(x﹣![]() )2﹣
)2﹣![]() a,∴△ACE的面積的最大值=﹣
a,∴△ACE的面積的最大值=﹣![]() a.
a.
∵△ACE的面積的最大值為![]() ,∴﹣
,∴﹣![]() a=
a=![]() ,解得:a=﹣
,解得:a=﹣![]() ;
;
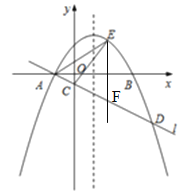
(3)以點A、D、P、Q為頂點的四邊形能成為矩形,令ax2﹣2ax﹣3a=ax+a,即ax2﹣3ax﹣4a=0,解得:x1=﹣1,x2=4,∴D(4,5a).
∵拋物線的對稱軸為直線x=1,設P(1,m),∴分兩種情況討論:
①若AD是矩形ADPQ的一條邊,則易得Q(﹣4,21a),m=21a+5a=26a,則P(1,26a).
∵四邊形ADPQ是矩形,∴∠ADP=90°,∴AD2+PD2=AP2,∴52+(5a)2+32+(26a﹣5a)2=22+(26a)2,即a2=![]() .
.
∵a<0,∴a=![]() ,∴P(1,
,∴P(1,![]() );
);
②若AD是矩形APDQ的對角線,則易得Q(2,﹣3a),m=5a﹣(﹣3a)=8a,則P(1,8a).
∵四邊形APDQ是矩形,∴∠APD=90°,∴AP2+PD2=AD2,∴(﹣1﹣1)2+(8a)2+(1﹣4)2+(8a﹣5a)2=52+(5a)2,即a2=![]() .
.
∵a<0,∴a=﹣![]() ,∴P(1,﹣4).
,∴P(1,﹣4).
綜上所述:點A、D、P、Q為頂點的四邊形能成為矩形,點P(1,﹣![]() )或(1,﹣4).
)或(1,﹣4).


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 上的動點,將
上的動點,將![]() 沿
沿![]() 折疊.
折疊.
(1)當點![]() 與點
與點![]() 重合時,如圖1.若
重合時,如圖1.若![]() ,
,![]() ,則
,則![]() 的周長為_____.
的周長為_____.
(2)定義:若在三角形中,期中一條邊是另一條邊的2倍,則稱這個三角形為“倍邊三角形”.當點![]() 與點
與點![]() 重合時,如圖2.若
重合時,如圖2.若![]() ,則
,則![]() 是倍邊三角形嗎?請說明理由.
是倍邊三角形嗎?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,將AB邊沿AD折疊,發現B點的對應點E正好在AC的垂直平分線上,則∠C=_______
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】兩個大小不同的等腰直角三角形三角板如圖 1 所示放置,圖 2 是由它抽像出的幾何圖形,B, C, E在同一 條直線上,連結DC.

(1)請找出圖 2 中的全等三角形,并給予證明(說明:結論中不得含有未標識的字 母);
(2)證明:DC ⊥ BE.
查看答案和解析>>
科目:初中數學 來源: 題型:
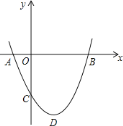
【題目】如圖,二次函數![]() .圖象的頂點為
.圖象的頂點為![]() ,其圖象與
,其圖象與![]() 軸的交點
軸的交點![]() 、
、![]() 的橫坐標分別為
的橫坐標分別為![]() 、
、![]() ,與
,與![]() 軸負半軸交于點
軸負半軸交于點![]() .下面五個結論:①
.下面五個結論:①![]() ;②
;②![]() ;③當
;③當![]() 時,
時,![]() 隨
隨![]() 值的增大而增大;④當
值的增大而增大;④當![]() 時,
時,![]() ;⑤只有當
;⑤只有當![]() 時,
時,![]() 是等腰直角三角形.那么,其中正確的結論______.(只填你認為正確結論的序號)
是等腰直角三角形.那么,其中正確的結論______.(只填你認為正確結論的序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在 Rt ![]() 中,
中,![]() ,
, ![]() ,點
,點 ![]() 為射線
為射線 ![]() 上一點,連接
上一點,連接 ![]() ,過點
,過點 ![]() 作線段
作線段 ![]() 的垂線
的垂線 ![]() ,在直線
,在直線 ![]() 上,分別在點
上,分別在點 ![]() 的兩側截取與線段
的兩側截取與線段 ![]() 相等的線段
相等的線段 ![]() 和
和 ![]() ,連接
,連接 ![]() ,
,![]() .
.
(1)當點 ![]() 在線段
在線段 ![]() 上時(點
上時(點 ![]() 不與點
不與點 ![]() ,
,![]() 重合),如圖1,
重合),如圖1,
①請你將圖形補充完整;
②線段 ![]() ,
,![]() 所在直線的位置關系為 ,線段
所在直線的位置關系為 ,線段 ![]() ,
,![]() 的數量關系為 ;
的數量關系為 ;

(2)當點 ![]() 在線段
在線段 ![]() 的延長線上時,如圖2,
的延長線上時,如圖2,
①請你將圖形補充完整;
②在(1)中②問的結論是否仍然成立?如果成立請進行證明,如果不成立,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:對于任何數a,符號[a]表示不大于a的最大整數.
例如:[5.7]=5,[5]=5,[﹣1.5]=﹣2.
(1)[﹣![]() ]= ;
]= ;
(2)如果[a]=3,那么a的取值范圍是 ;
(3)如果[![]() ]=﹣3,求滿足條件的所有整數x.
]=﹣3,求滿足條件的所有整數x.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(閱讀)如圖1,四邊形OABC中,OA=a,OC=3,BC=2,
∠AOC=∠BCO=90°,經過點O的直線l將四邊形分成兩部分,直線l與OC所成的角設為θ,將四邊形OABC的直角∠OCB沿直線l折疊,點C落在點D處,我們把這個操作過程記為FZ[θ,a].
(理解)
若點D與點A重合,則這個操作過程為FZ[45°,3];
(嘗試)
(1)若點D恰為AB的中點(如圖2),求θ;
(2)經過FZ[45°,a]操作,點B落在點E處,若點E在四邊形OABC的邊AB上,求出a的值;若點E落在四邊形OABC的外部,直接寫出a的取值范圍.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com