
探索:如圖①,以△ABC的邊AB、AC為直角邊,A為直角頂點,向外作等腰直角△ABD和等腰直角△ACE,連結BE、CD,試確定BE與CD有怎樣數量關系,并說明理由.
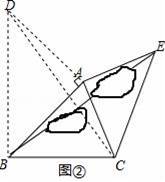
應用:如圖②,要測量池塘兩岸B、E兩地之間的距離,已知測得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的長.
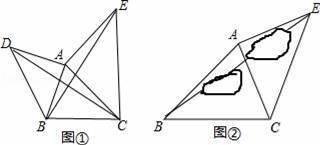

【考點】勾股定理的應用;全等三角形的判定與性質.
【分析】根據全等三角形的判定方法得出△CAD≌△EAB(SAS),進而利用全等三角形的性質結合勾股定理得出DC的長,進而得出答案.
【解答】解:探索:BE=CD,
理由:∵∠BAD=∠CAE=90°,
∴∠CAD=∠EAB,
在△CAD和△EAB中
∵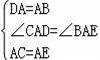
 ,
,
∴△CAD≌△EAB(SAS);
應用:如圖②,過點A作AD⊥AB,且AD=AB,連接BD,
由探索,得△CAD≌△EAB,
∴BE=DC,
∵AD=AB=100m,∠DAB=90°,
∴∠ABD=45°,BD=100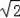
 m,
m,
∵∠ABC=45°,
∴∠DBC=90°,
在Rt△DBC中,BC=100m,BD=100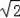
 m,
m,
∴CD=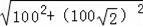
 =100
=100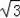
 (m),
(m),
則BE=100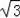
 m,
m,
答:BE的長為100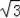
 m.
m.

【點評】此題主要考查了全等三角形的判定與性質以及勾股定理應用,正確得出△CAD≌△EAB(SAS)是解題關鍵.


 芝麻開花課程新體驗系列答案
芝麻開花課程新體驗系列答案 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案科目:初中數學 來源: 題型:
在一個不透明的盒子里裝有只有顏色不同的黑、白兩種球共40個,小李做摸球實驗,她將盒子里面的球攪勻后從中隨機摸出一個球記下顏色,再把它放回盒子中,不斷重復上述過程,如表是實驗中的一組統計數據:
| 摸球的次數n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次數m | 63 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的頻率 | 0.63 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)請估計:當實驗次數為10000次時,摸到白球的頻率將會接近 ;(精確到0.1)
(2)假如你摸一次,你摸到白球的概率P(摸到白球)= ;
(3)如何通過增加或減少這個不透明盒子內球的具體數量,使得在這個盒子里每次摸到白球的概率為0.5?
查看答案和解析>>
科目:初中數學 來源: 題型:
下列說法正確的是 ( )
A.為了了解某中學800名學生的視力情況,從中隨機抽取了50名學生進行調查,在此次調查中,樣本容量為50名學生的視力
B.若一個游戲的中獎率是1%,則做100次這樣的游戲一定會中獎
C.了解無錫市每天的流動人口數,采用抽查方式
D.“擲一枚硬幣,正面朝上”是必然事件
查看答案和解析>>
科目:初中數學 來源: 題型:
一輛汽車從A地駛往B地,前
 路為普通公路,其余路段為高速公路,已知汽車在普通公路上行駛的速度為60km/h,在高速路上行駛的速度為100km/h,汽車從A地到B地一共行駛了2.2h,普通公路和高速公路各是多少km?
路為普通公路,其余路段為高速公路,已知汽車在普通公路上行駛的速度為60km/h,在高速路上行駛的速度為100km/h,汽車從A地到B地一共行駛了2.2h,普通公路和高速公路各是多少km?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com