
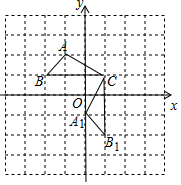
 已知如圖,在直角坐標(biāo)平面內(nèi),△ABC的三個頂點的坐標(biāo)分別為A(-1,2),B(-2,1)(正方形網(wǎng)格中每個小正方形的邊長是1個單位長度).
已知如圖,在直角坐標(biāo)平面內(nèi),△ABC的三個頂點的坐標(biāo)分別為A(-1,2),B(-2,1)(正方形網(wǎng)格中每個小正方形的邊長是1個單位長度).分析 (1)由旋轉(zhuǎn)的性質(zhì)即可得;
(2)根據(jù)勾股定理求得半徑AC的長,由扇形面積公式可得答案.
解答 解:(1)由圖可知,△A1B1C1是△ABC繞點C逆時針旋轉(zhuǎn)90度得到的,B1的坐標(biāo)是(1,-2),
故答案為:C,90,(1,-2);
(2)∵AC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∴線段AC旋轉(zhuǎn)過程中所掃過的面積$\frac{90°•π•(\sqrt{5})^{2}}{360°}$=$\frac{5π}{4}$.
點評 本題主要考查坐標(biāo)與圖形的變化-旋轉(zhuǎn)和扇形的面積的計算,熟練掌握旋轉(zhuǎn)的定義和扇形的面積公式是解題的關(guān)鍵.


 名校名師培優(yōu)作業(yè)本加核心試卷系列答案
名校名師培優(yōu)作業(yè)本加核心試卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 6$\sqrt{2}$ | B. | 2$\sqrt{12}$ | C. | 6 | D. | 8 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
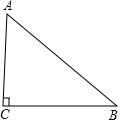 如圖,已知△ABC,∠C=90°,AC<BC.D為BC上一點,且到A,B兩點的距離相等.
如圖,已知△ABC,∠C=90°,AC<BC.D為BC上一點,且到A,B兩點的距離相等.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com