
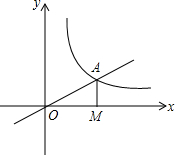
 如圖,正比例y=$\frac{1}{2}$x的圖象與y=$\frac{k}{x}$(k≠0)在第一象限的圖象交于A點,過A點作x軸的垂線,垂足為M,已知△OAM的面積為1.如果B為及比例函數(shù)在第一象限圖象上的點(點B與點A不重合),且B點的橫坐標為1,P為x軸上一點,求使PA+PB的值最小時點P坐標.
如圖,正比例y=$\frac{1}{2}$x的圖象與y=$\frac{k}{x}$(k≠0)在第一象限的圖象交于A點,過A點作x軸的垂線,垂足為M,已知△OAM的面積為1.如果B為及比例函數(shù)在第一象限圖象上的點(點B與點A不重合),且B點的橫坐標為1,P為x軸上一點,求使PA+PB的值最小時點P坐標. 分析 根據(jù)反比例函數(shù)圖象上的點的橫縱坐標的乘積為函數(shù)的系數(shù)和△OAM的面積為1可得k=2,即求得反比例函數(shù)的解析式.要使PA+PB最小,需作出A點關(guān)于x軸的對稱點C,連接BC,交x軸于點P,P為所求點.A點關(guān)于x軸的對稱點C(2,-1),而B為(1,2),故BC的解析式為y=-3x+5,當y=0時,x=$\frac{5}{3}$,即可得出答案.
解答 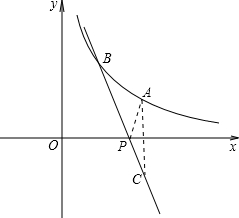 解:設(shè)A點的坐標為(a,b),則b=$\frac{k}{a}$,
解:設(shè)A點的坐標為(a,b),則b=$\frac{k}{a}$,
∴ab=k,
∵$\frac{1}{2}$ab=1,
∴$\frac{1}{2}$k=1
∴k=2
∴反比例函數(shù)的解析式為y=$\frac{2}{x}$,
根據(jù)題意畫出圖形,如圖所示:
聯(lián)立得$\left\{\begin{array}{l}{y=\frac{2}{x}}\\{y=\frac{1}{2}x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,
∴A為(2,1),
設(shè)A點關(guān)于x軸的對稱點為C,則C點的坐標為(2,-1).
∵點B的橫坐標為1,
∴B為(1,2),
設(shè)直線BC的解析式為y=mx+n
將B和C的坐標代入得:$\left\{\begin{array}{l}{2m+n=-1}\\{m+n=2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=-3}\\{n=5}\end{array}\right.$,
∴BC的解析式為y=-3x+5,
當y=0時,x=$\frac{5}{3}$,
∴P點為($\frac{5}{3}$,0).
點評 此題考查了反比例函數(shù)和一次函數(shù)解析式的確定、圖形的面積求法、軸對稱等知識及綜合應(yīng)用知識、解決問題的能力.有點難度.


 考前必練系列答案
考前必練系列答案科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
 如圖,一個瓶子的容積為1L,瓶內(nèi)裝著一些溶液.當瓶子正放時,瓶內(nèi)溶液的高度為30cm,將瓶子倒放時,空余部分的高度為10cm.現(xiàn)將瓶內(nèi)的溶液全部倒入一個圓柱形的杯子里,杯內(nèi)溶液的高度為15cm,則圓柱形杯子的內(nèi)底面半徑約為( )
如圖,一個瓶子的容積為1L,瓶內(nèi)裝著一些溶液.當瓶子正放時,瓶內(nèi)溶液的高度為30cm,將瓶子倒放時,空余部分的高度為10cm.現(xiàn)將瓶內(nèi)的溶液全部倒入一個圓柱形的杯子里,杯內(nèi)溶液的高度為15cm,則圓柱形杯子的內(nèi)底面半徑約為( )| A. | 2.8cm | B. | 4.0cm | C. | 5.0cm | D. | 6.2cm |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 如圖,已知直線y=$\frac{1}{3}$x+1與x軸交于點A,與y軸交于點B,將△AOB繞點O順時針旋轉(zhuǎn)90°后得到△COD.
如圖,已知直線y=$\frac{1}{3}$x+1與x軸交于點A,與y軸交于點B,將△AOB繞點O順時針旋轉(zhuǎn)90°后得到△COD.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
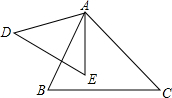 如圖所示,在△ABC與△ADE中,AB•ED=AE•BC,要使△ABC與△ADE相似,還需要添加一個條件,這個條件是∠B=∠E(答案不唯一)(只加一個即可)并證明.
如圖所示,在△ABC與△ADE中,AB•ED=AE•BC,要使△ABC與△ADE相似,還需要添加一個條件,這個條件是∠B=∠E(答案不唯一)(只加一個即可)并證明.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
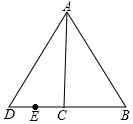 如圖,已知Rt△ABC中,∠ACB=90°,∠BAC=30°,延長BC至D使CD=BC,連接AD.
如圖,已知Rt△ABC中,∠ACB=90°,∠BAC=30°,延長BC至D使CD=BC,連接AD.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com