
 以下是根據北京市統計局公布的2010—2013年北京市城鎮居民人均可支配收入和農民人均現金收入的數據繪制的統計圖的一部分:
以下是根據北京市統計局公布的2010—2013年北京市城鎮居民人均可支配收入和農民人均現金收入的數據繪制的統計圖的一部分:
根據以上信息,解答下列問題:
(1)2 012年農民人均現金收入比2011年城鎮居民人均可支配收入的一半少0.05萬元,則2012年農民人
012年農民人均現金收入比2011年城鎮居民人均可支配收入的一半少0.05萬元,則2012年農民人
均現金收入是 萬元,請根據以上信息補全條形統計圖,并標明相應的數據(結果精確到0.1);
(2)在2010—2013年這四年中,北京市城鎮居民人均可支配收入和農民人均現金收入相差數額最大的年
份是 年;
(3)①2011—2013年城鎮居民人均可支配收入的年平均增長率最接近 ;
A.14% B.11% C.10%  D.9%
D.9%
②若2014年城鎮居民人均可支配收入按①中的年平均增長率增長,請預測2014年的城鎮居民人均可
支配收入為 萬元(結果精確到0.1)。
 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
如圖,在平面直角坐標系 中,以點
中,以點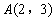 為頂點任作一直角
為頂點任作一直角 ,使其兩邊分別與
,使其兩邊分別與 軸、
軸、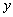 軸
軸
的正半軸交于點 、
、 ,連接
,連接 ,過點
,過點 作
作 于點
于點 ,設點
,設點 的橫坐標為
的橫坐標為 ,
, 的長為
的長為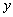 ,
,
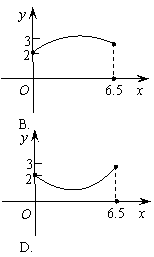
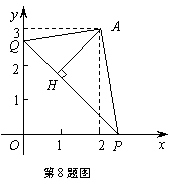
則下列圖象中,能表示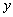 與
與 的函數關系的圖象大致是( )
的函數關系的圖象大致是( )
 | |||||
 | |||||
 | |||||
查看答案和解析>>
科目:初中數學 來源: 題型:
定義1:在 中,若頂點
中,若頂點 ,
,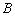 ,
, 按逆時針方向排列,則規定它的面積為“有向面積”;若頂點
按逆時針方向排列,則規定它的面積為“有向面積”;若頂點
 ,
, ,
, 按順時針方向排列,則規定它的面積的相反數為
按順時針方向排列,則規定它的面積的相反數為 的“有向面積”。“有
的“有向面積”。“有 向面積”用
向面積”用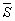 表示,
表示,


 例如圖1中,
例如圖1中,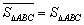 ,圖2中,
,圖2中,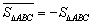 。
。
定義2:在平面內任取一個 和點
和點 (點
(點 不在
不在 的三邊所在直線上),稱有序數組(
的三邊所在直線上),稱有序數組( ,
,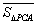 ,
, )為點
)為點 關于
關于 的“
的“ 面積坐標”,記作
面積坐標”,記作 ,例如圖3中,菱形
,例如圖3中,菱形 的邊長為2,
的邊長為2,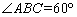 ,則
,則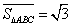 ,點
,點 關于
關于 的“面積坐標”
的“面積坐標”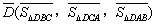 為
為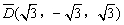 。
。
 在圖3中,我們知道
在圖3中,我們知道 ,利用“有向面積”,我們也可以把上式表示為:
,利用“有向面積”,我們也可以把上式表示為:
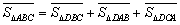 。
。
應用新知:
(1)如圖4,正方形 的邊長為1,則
的邊長為1,則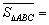 ,點
,點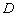 關于
關于 的“面積坐標”是 ;
的“面積坐標”是 ;
探究發現:
(2)在平面直角坐標系 中,點
中,點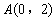 ,
,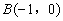 .
.
①若點 是第二象限內任意一點(不在直線
是第二象限內任意一點(不在直線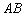 上),設點
上),設點 關于
關于 的“面積坐標”為
的“面積坐標”為 ,
,
試探究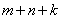 與
與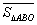 之間有怎樣的數量關系,并說明理由;
之間有怎樣的數量關系,并說明理由;
②若點 是第四象限內任意一點,請直接寫出點
是第四象限內任意一點,請直接寫出點 關于
關于 的“面積坐標”(用
的“面積坐標”(用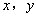 表示);
表示);
解決問題:
(3)在(2)的條件下,點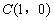 ,
, ,點
,點 在拋物線
在拋物線 上,求當
上,求當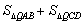 的值最小時,點
的值最小時,點 的橫坐標。
的橫坐標。
查看答案和解析>>
科目:初中數學 來源: 題型:
已知:等邊三角形ABC中,點D、E、F分別為邊AB、AC、BC的中點,點M在直線BC上,以點M為旋轉中心,將線段MD順時針旋轉60º至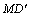 ,連接
,連接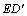 .
.
(1)如圖1,當點M在點B左側時,線段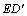 與MF的數量關系是__________;
與MF的數量關系是__________;
(2)如圖2,當點M在BC邊上時,(1)中的結論是否依然成立?如果成立,請利用圖2證明,如果不成立,請說明理由;
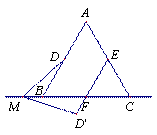
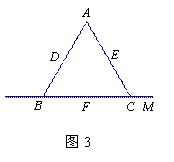
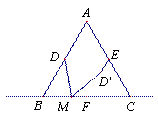 (3)當點M在點C右側時,請你在圖3中畫出相應的圖形,直接判斷(1)中的結論是否依然成立?不必給出證明或說明理由.
(3)當點M在點C右側時,請你在圖3中畫出相應的圖形,直接判斷(1)中的結論是否依然成立?不必給出證明或說明理由.
|
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com