

分析 感知:先利用矩形性質得:∠D=∠C=90°,再利用同角的余角相等得:∠DAE=∠FEC,根據已知邊的長度計算出AD=CE=3,則由ASA證得:△ADE≌△ECF;
探究:利用兩角相等證明△PDE∽△ECF;
應用:作輔助線,構建如圖②一樣的相似三角形,利用探究得:△PDE∽△EGF,則$\frac{DE}{FG}=\frac{PE}{EF}$,所以$\frac{PE}{EF}=\frac{1}{3}$,
再利用△PEF的面積是3,列式可得:PE•EF=6,兩式結合可求得PE的長,利用勾股定理求PD,從而得出AP的長.
解答 證明:感知:如圖①,∵四邊形ABCD為矩形,
∴∠D=∠C=90°,
∴∠DAE+∠DEA=90°,
∵EF⊥AE,
∴∠AEF=90°,
∴∠DEA+∠FEC=90°,
∴∠DAE=∠FEC,
∵DE=1,CD=4,
∴CE=3,
∵AD=3,
∴AD=CE,
∴△ADE≌△ECF(ASA);
探究:如圖②,∵四邊形ABCD為矩形,
∴∠D=∠C=90°,
∴∠DPE+∠DEP=90°,
∵EF⊥PE,
∴∠PEF=90°,
∴∠DEP+∠FEC=90°,
∴∠DPE=∠FEC,
∴△PDE∽△ECF;
應用:如圖③,過F作FG⊥DC于G,
∵四邊形ABCD為矩形,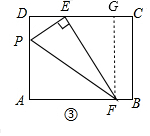
∴AB∥CD,
∴FG=BC=3,
∵PE⊥EF,
∴S△PEF=$\frac{1}{2}$PE•EF=3,
∴PE•EF=6,
同理得:△PDE∽△EGF,
∴$\frac{DE}{FG}=\frac{PE}{EF}$,
∴$\frac{PE}{EF}=\frac{1}{3}$,
∴EF=3PE,
∴3PE2=6,
∴PE=$±\sqrt{2}$,
∵PE>0,
∴PE=$\sqrt{2}$,
在Rt△PDE中,由勾股定理得:PD=1,
∴AP=AD-PD=3-1=2,
故答案為:2.
點評 本題考查了矩形、相似三角形的性質和判定、全等三角形的性質和判定;難度適中,運用類比的方法解決問題,從感知、探究和應用,逐漸引導學生利用全等或相似解決問題,如果圖形中沒有全等或相似的三角形,要作輔助線構建,此類題培養了學生的思維能力.


科目:初中數學 來源: 題型:填空題
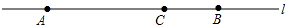 如圖,已知點A、點B是直線上的兩點,AB=12厘米,點C在線段AB上,且AC=8厘米.點P、點Q是直線上的兩個動點,點P的速度為1厘米/秒,點Q的速度為2厘米/秒.點P、Q分別從點C、點B同時出發,在直線上運動,則經過2、10、$\frac{2}{3}$或$\frac{10}{3}$秒時線段PQ的長為6厘米.
如圖,已知點A、點B是直線上的兩點,AB=12厘米,點C在線段AB上,且AC=8厘米.點P、點Q是直線上的兩個動點,點P的速度為1厘米/秒,點Q的速度為2厘米/秒.點P、Q分別從點C、點B同時出發,在直線上運動,則經過2、10、$\frac{2}{3}$或$\frac{10}{3}$秒時線段PQ的長為6厘米.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,在正方形ABCD中,△BPC是等邊三角形,BP、CP的延長線分別交AD于點E、F,連結BD、DP,BD與CF相交于點H.給出下列結論:①△BDE∽△DPE;②$\frac{FP}{PH}=\frac{3}{5}$;③DP2=PH•PB;④tan∠DBE=2-$\sqrt{3}$.其中正確結論的序號是①③④.
如圖,在正方形ABCD中,△BPC是等邊三角形,BP、CP的延長線分別交AD于點E、F,連結BD、DP,BD與CF相交于點H.給出下列結論:①△BDE∽△DPE;②$\frac{FP}{PH}=\frac{3}{5}$;③DP2=PH•PB;④tan∠DBE=2-$\sqrt{3}$.其中正確結論的序號是①③④.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | x≥1 | B. | x≥-1 | C. | -1≤x≤1 | D. | x≥1或x≥-1 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com