
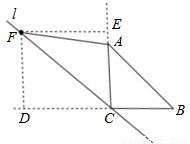
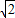 ,又AB=AF;所以,在直角△AEF中,可運用勾股定理求得DF的長即為點F到BC的距離.
,又AB=AF;所以,在直角△AEF中,可運用勾股定理求得DF的長即為點F到BC的距離.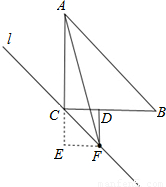 ∴四邊形CDFE是正方形,
∴四邊形CDFE是正方形,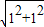 =
=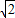 ,
,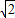 ;
;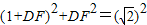 ,
,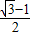 ;
;
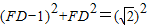 ,
,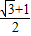 ;
;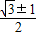 .
.

 直通貴州名校周測月考直通名校系列答案
直通貴州名校周測月考直通名校系列答案科目:初中數學 來源: 題型:
 16、如圖,在等腰Rt△ABC中,∠A=90°,AC=9,點O在AC上,且AO=2,點P是AB上一動點,連接OP將線段OP繞O逆時針旋轉90°得到線段OD,要使點D恰好落在BC上,則AP的長度等于
16、如圖,在等腰Rt△ABC中,∠A=90°,AC=9,點O在AC上,且AO=2,點P是AB上一動點,連接OP將線段OP繞O逆時針旋轉90°得到線段OD,要使點D恰好落在BC上,則AP的長度等于查看答案和解析>>
科目:初中數學 來源: 題型:
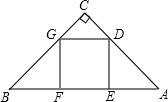 點G在邊BC上.
點G在邊BC上.| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•懷化)如圖,在等腰Rt△ABC中,∠C=90°,正方形DEFG的頂點D在邊AC上,點E、F在邊AB上,點G在邊BC上.
(2013•懷化)如圖,在等腰Rt△ABC中,∠C=90°,正方形DEFG的頂點D在邊AC上,點E、F在邊AB上,點G在邊BC上.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com