
分析 (1)根據題意可以列出相應的方程,從而可以解答本題;
(2)根據題意可以列出相應的不等式,從而可以得到有多少種購買方案和哪種方案,最省錢.
解答 解:(1)設購買鐵撮子的單價為x元,
3(1.5x-2)=4x,
解得,x=12,
1.5x-2=16
即掃帚、鐵撮子兩種工具的單價各是16元,12元;
(2)設購買鐵撮子a把,
$\left\{\begin{array}{l}{12a+16(100-a)≤1440}\\{100-a≥50}\\{100-a≤3a}\end{array}\right.$,
解得,40≤a≤50,
∴有11種購買方案,
花費為:12a+16(100-a)=-4a+1600,
∴當a=50時,花費最少,此時,-4a+1600=-4×50+1600=1400,
即當購買買鐵撮子50把,掃帚50把時最省錢.
點評 本題考查一次函數的應用、一元一次方程的應用、一元一次不等式的應用,解答本題的關鍵是明確題意,找出所求問題條件,利用方程和不等式的思想解答問題.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:解答題
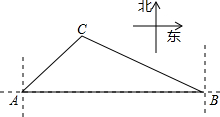 如圖,一艘海輪在A點時測得燈塔C在它的北偏東45°方向上,它沿正東方向航行80海里后到達B處.此時燈塔C在它的北偏西60°方向上.
如圖,一艘海輪在A點時測得燈塔C在它的北偏東45°方向上,它沿正東方向航行80海里后到達B處.此時燈塔C在它的北偏西60°方向上.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
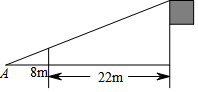 如圖,為測量學校旗桿的高度,小東用長為3.2m的竹竿做測量工具,移動竹竿使竹竿和旗桿兩者頂端的影子恰好落在地面的同一點A,此時,竹竿與點A相距8m,與旗桿相距22m,則旗桿的高為( )
如圖,為測量學校旗桿的高度,小東用長為3.2m的竹竿做測量工具,移動竹竿使竹竿和旗桿兩者頂端的影子恰好落在地面的同一點A,此時,竹竿與點A相距8m,與旗桿相距22m,則旗桿的高為( )| A. | 6m | B. | 8.8m | C. | 12m | D. | 30m |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
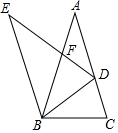 如圖,已知△ABC與△BED都是頂角為36°的等腰三角形,點D是邊AC上一點,且滿足BC2=CD•AC,DE與AB相交于點F,則圖中有( )對相似三角形.
如圖,已知△ABC與△BED都是頂角為36°的等腰三角形,點D是邊AC上一點,且滿足BC2=CD•AC,DE與AB相交于點F,則圖中有( )對相似三角形.| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com