
分析 首先把分式的分子和分母分解因式,把除法轉(zhuǎn)化為乘法,計(jì)算乘法即可化簡(jiǎn),然后根據(jù)x:y=2:3,則設(shè)x=2m,則y=3m,代入所求的式子進(jìn)行化簡(jiǎn)即可.
解答 解:原式=$\frac{(x+y)(x-y)}{xy}$÷$\frac{(x+y)(x-y)^{3}}{{x}^{3}}$÷$\frac{x}{{y}^{2}}$
=$\frac{(x+y)(x-y)}{xy}$•$\frac{{x}^{3}}{(x+y)(x-y)^{3}}$•$\frac{{y}^{2}}{x}$
=$\frac{xy}{(x-y)^{2}}$,
∵x:y=2:3,
∴設(shè)x=2m,則y=3m,
則原式=$\frac{6{m}^{2}}{{m}^{2}}$=6.
點(diǎn)評(píng) 本題考查了分式的化簡(jiǎn)求值以及二次根式的化簡(jiǎn),正確把分式的分子和分母分解因式是本題的關(guān)鍵.


 名校課堂系列答案
名校課堂系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2+$\sqrt{2}$=2$\sqrt{2}$ | C. | $\sqrt{12}$-$\sqrt{10}$=$\sqrt{2}$ | D. | 3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
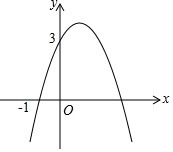 已知二次函數(shù)y=-x2+bx+c的圖象如圖所示,它與x軸的一個(gè)交點(diǎn)坐標(biāo)為(-1,0),與y軸的交點(diǎn)坐標(biāo)為(0,3).
已知二次函數(shù)y=-x2+bx+c的圖象如圖所示,它與x軸的一個(gè)交點(diǎn)坐標(biāo)為(-1,0),與y軸的交點(diǎn)坐標(biāo)為(0,3).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
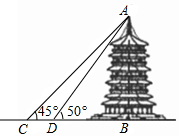 某中學(xué)九年級(jí)數(shù)學(xué)興趣小組想測(cè)量建筑物AB的高度,他們?cè)贑處仰望建筑物頂端A,測(cè)得仰角為45°,再往建筑物的方向前進(jìn)3.8米到達(dá)D處,測(cè)得仰角為50°,AB⊥CB,求建筑物的高度.(測(cè)角器的高度忽略不計(jì),結(jié)果保留小數(shù)點(diǎn)后一位,參考數(shù)據(jù)sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
某中學(xué)九年級(jí)數(shù)學(xué)興趣小組想測(cè)量建筑物AB的高度,他們?cè)贑處仰望建筑物頂端A,測(cè)得仰角為45°,再往建筑物的方向前進(jìn)3.8米到達(dá)D處,測(cè)得仰角為50°,AB⊥CB,求建筑物的高度.(測(cè)角器的高度忽略不計(jì),結(jié)果保留小數(shù)點(diǎn)后一位,參考數(shù)據(jù)sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com