
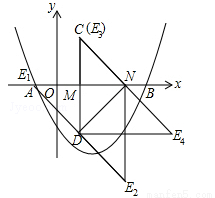
(本題滿分12分)如圖,二次函數(shù)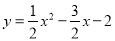 的圖像與x軸交于點(diǎn)A,B.點(diǎn)M、N在x軸上,點(diǎn)N在點(diǎn)M右側(cè),MN=2.以MN為直角邊向上作等腰直角三角形CMN,∠CMN=90°.設(shè)點(diǎn)M的橫坐標(biāo)為m.
的圖像與x軸交于點(diǎn)A,B.點(diǎn)M、N在x軸上,點(diǎn)N在點(diǎn)M右側(cè),MN=2.以MN為直角邊向上作等腰直角三角形CMN,∠CMN=90°.設(shè)點(diǎn)M的橫坐標(biāo)為m.
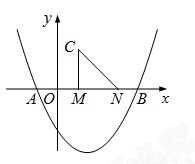
(1)當(dāng)點(diǎn)C在這條拋物線上時(shí),求m的值.
(2)將線段CN繞點(diǎn)N逆時(shí)針旋轉(zhuǎn)90°后,得到對(duì)應(yīng)線段DN.
①當(dāng)點(diǎn)D在這條拋物線的對(duì)稱軸上時(shí),求點(diǎn)D的坐標(biāo).
②以DN為直角邊作等腰直角三角形DNE,當(dāng)點(diǎn)E在這條拋物線的對(duì)稱軸上時(shí),求m的值.
(1)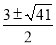 ;(2)①(
;(2)①(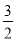 ,-2);②
,-2);②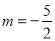 或
或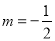 或
或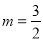 或
或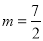 .
.
【解析】
試題分析:(1)先根據(jù)等腰直角三角形的性質(zhì)求出點(diǎn)C的坐標(biāo)為(m,2),再將C的坐標(biāo)代入 ,即可求出m的值;
,即可求出m的值;
(2)①先由旋轉(zhuǎn)的性質(zhì)得出點(diǎn)D的坐標(biāo)為(m,﹣2),再根據(jù)二次函數(shù)的性質(zhì)求出拋物線 的對(duì)稱軸為直線
的對(duì)稱軸為直線 ,然后根據(jù)點(diǎn)D在直線
,然后根據(jù)點(diǎn)D在直線 上,即可求出點(diǎn)D的坐標(biāo);
上,即可求出點(diǎn)D的坐標(biāo);
②以DN為直角邊作等腰直角三角形DNE時(shí),分別以D、N為直角頂點(diǎn),在DN的兩側(cè)分別作出等腰直角三角形DNE,E點(diǎn)的位置分四種情況討論.針對(duì)每一種情況,都可以先根據(jù)等腰直角三角形的性質(zhì)求出點(diǎn)E的坐標(biāo),然后根據(jù)點(diǎn)E在直線 上,列出關(guān)于m的方程,解方程即可求出m的值.
上,列出關(guān)于m的方程,解方程即可求出m的值.
試題解析:(1)∵△CMN是等腰直角三角形CMN,∠CMN=90°,∴CM=MN=2,∴點(diǎn)C的坐標(biāo)為(m,2),∵點(diǎn)C(m,2)在拋物線上,∴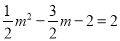 ,解得
,解得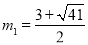 ,
,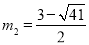 .∴點(diǎn)C在這條拋物線上時(shí),m的值為
.∴點(diǎn)C在這條拋物線上時(shí),m的值為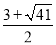 或
或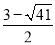 ;
;
(2)①∵將線段CN繞點(diǎn)N逆時(shí)針旋轉(zhuǎn)90°后,得到對(duì)應(yīng)線段DN,∴∠CND=90°,DN=CN=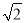 CM=
CM=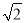 MN,∴CD=
MN,∴CD=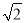 CN=2CM=2MN,∴DM=CM=MN,∠DMN=90°,∴點(diǎn)D的坐標(biāo)為(m,﹣2).又∵拋物線
CN=2CM=2MN,∴DM=CM=MN,∠DMN=90°,∴點(diǎn)D的坐標(biāo)為(m,﹣2).又∵拋物線 的對(duì)稱軸為直線
的對(duì)稱軸為直線 ,點(diǎn)D在這條拋物線的對(duì)稱軸上,∴點(diǎn)D的坐標(biāo)為(
,點(diǎn)D在這條拋物線的對(duì)稱軸上,∴點(diǎn)D的坐標(biāo)為(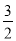 ,﹣2);
,﹣2);
②如圖,以DN為直角邊作等腰直角三角形DNE,E點(diǎn)的位置有四種情況:如果E點(diǎn)在E1的位置時(shí),∵點(diǎn)D的坐標(biāo)為(m,﹣2),MN=ME1=2,點(diǎn)N的坐標(biāo)為(m+2,0),∴點(diǎn)E1的(m﹣2,0),∵點(diǎn)E1在拋物線 的對(duì)稱軸直線
的對(duì)稱軸直線 上,∴
上,∴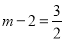 ,解得
,解得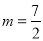 ;
;
如果E點(diǎn)在E2的位置時(shí),∵點(diǎn)D的坐標(biāo)為(m,﹣2),點(diǎn)N的坐標(biāo)為(m+2,0),∴點(diǎn)E2的(m+2,﹣4),∵點(diǎn)E2在拋物線 的對(duì)稱軸直線
的對(duì)稱軸直線 上,∴
上,∴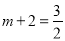 ,解得
,解得 ;
;
如果E點(diǎn)在E3的位置時(shí),∵點(diǎn)D的坐標(biāo)為(m,﹣2),∴點(diǎn)E3的(m,2),∵點(diǎn)E3在拋物線 的對(duì)稱軸直線
的對(duì)稱軸直線 上,∴
上,∴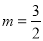 ;
;
如果E點(diǎn)在E4的位置時(shí),∵點(diǎn)D的坐標(biāo)為(m,﹣2),點(diǎn)N的坐標(biāo)為(m+2,0),∴點(diǎn)E4的(m+4,﹣2),∵點(diǎn)E4在拋物線 的對(duì)稱軸直線
的對(duì)稱軸直線 上,∴
上,∴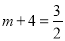 ,解得
,解得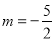 ;
;
綜上可知,當(dāng)點(diǎn)E在這條拋物線的對(duì)稱軸上時(shí),所有符合條件的m的值為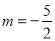 或
或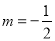 或
或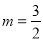 或
或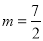 .
.
考點(diǎn):二次函數(shù)綜合題.


 靈星計(jì)算小達(dá)人系列答案
靈星計(jì)算小達(dá)人系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源:2014-2015學(xué)年江蘇省宜興市九年級(jí)上學(xué)期第二次質(zhì)量抽測(cè)數(shù)學(xué)試卷(解析版) 題型:填空題
拋物線y=-x2的頂點(diǎn)坐標(biāo)為________;若點(diǎn)A(3,m)是此拋物線上一點(diǎn),則m= ____;把此拋物線向下平移4個(gè)單位得到的拋物線的函數(shù)關(guān)系式是 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源:2014-2015學(xué)年江蘇省宜興市九年級(jí)11月階段性檢測(cè)數(shù)學(xué)試卷(解析版) 題型:選擇題
下列函數(shù)中二次函數(shù)是( )
A.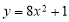 B.
B.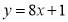 C.
C.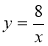 D.
D.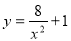
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源:2014-2015學(xué)年江蘇省揚(yáng)州市寶應(yīng)縣九年級(jí)上學(xué)期期末測(cè)試數(shù)學(xué)試卷(解析版) 題型:填空題
如圖,在矩形ABCD中,對(duì)角線AC、BD相交于點(diǎn)O,∠AOB=60°,點(diǎn)E、F分別是BO、BC的中點(diǎn),若AB=6cm,則△BEF的周長(zhǎng)為
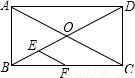
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源:2014-2015學(xué)年江蘇省揚(yáng)州市寶應(yīng)縣九年級(jí)上學(xué)期期末測(cè)試數(shù)學(xué)試卷(解析版) 題型:選擇題
如圖,已知AB為⊙O的直徑,點(diǎn)C、D在⊙O上,∠ABC=50°,則∠D的度數(shù)為( )

A.30° B.40° C.50° D.60°
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源:2014-2015學(xué)年江蘇省鹽城市鹽都區(qū)九年級(jí)上學(xué)期期末考試數(shù)學(xué)試卷(解析版) 題型:解答題
(本題滿分10分)鹽城公共自行車項(xiàng)目現(xiàn)已全部建成,鹽城市區(qū)250個(gè)站點(diǎn),累計(jì)投放6000輛自行車,為人們的生活帶來(lái)了方便.圖(1)所示的是自行車的實(shí)物圖.圖(2)是一輛自行車的部分幾何示意圖,其中車架檔AC的長(zhǎng)為45cm,且∠CAB=75°,∠CBA=50°.(參考數(shù)據(jù):sin75°≈0.96,cos75°≈0.26,tan75°≈3.73 ,sin50°≈0.76,cos50°≈0.64,tan50°≈1.19)

(1)求車座固定點(diǎn)C到車架檔AB的距離;
(2)求車架檔AB的長(zhǎng)(結(jié)果精確到1cm).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源:2014-2015學(xué)年江蘇省鹽城市鹽都區(qū)九年級(jí)上學(xué)期期末考試數(shù)學(xué)試卷(解析版) 題型:填空題
如圖,沿一條母線將圓錐側(cè)面剪開并展平,得到一個(gè)扇形,若圓錐的底面圓的半徑r=2cm,扇形的圓心角θ=120°,則該圓錐的母線長(zhǎng)l為 cm.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源:2014-2015學(xué)年江蘇省蘇州市九年級(jí)上學(xué)期期末考試數(shù)學(xué)試卷(解析版) 題型:解答題
如圖,已知AB是⊙O的直徑,AB=8,點(diǎn)C在半徑OA上(點(diǎn)C與點(diǎn)O、A不重合),過點(diǎn)C作AB的垂線交⊙O于點(diǎn)D,連結(jié)OD,過點(diǎn)B作OD的平行線交⊙O于點(diǎn)E、交射線CD于點(diǎn)F.
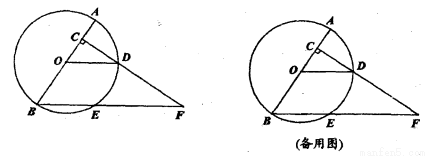
(1)若ED=BE,求∠F的度數(shù):
(2)設(shè)線段OC=a,求線段BE和EF的長(zhǎng)(用含a的代數(shù)式表示);
(3)設(shè)點(diǎn)C關(guān)于直線OD的對(duì)稱點(diǎn)為P,若△PBE為等腰三角形,求OC的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源:2014-2015學(xué)年湖南省耒陽(yáng)市九年級(jí)上學(xué)期期末考試數(shù)學(xué)試卷(解析版) 題型:填空題
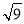 的平方根是
的平方根是
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com