Question

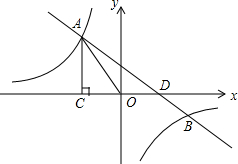
11．如圖，已知反比例函數y₁=$\frac{k}{x}$（k＜0）的圖象與一次函數y₂=ax+1（a≠0）的圖象相交于A、B兩點，AC⊥x軸于點C，若△OAC的面積為1，且A點的橫坐標為-1．
（1）求反比例函數與一次函數的表達式；
（2）直接寫出B點的坐標，并結合圖象指出當x為何值時，反比例函數y₁的值小于一次函數y₂的值．

Answer 1

分析 （1）根據反比例函數系數k的幾何意義可求出k的值，然后根據條件可求出點A的坐標，然后運用待定系數法就可解決問題；
（2）只需通過解反比例函數與一次函數的表達式組成的方程組，就可求出點B的坐標，然后運用數形結合的思想，結合圖象就可解決問題．

解答 解：（1）∵點A在y₁=$\frac{k}{x}$（k＜0）的圖象上，S_△OAC=1，
∴$|\begin{array}{l}{k}\end{array}|$=2×1=2．
∵k＜0，∴k=-2，
∴反比例函數的表達式為y₁=-$\frac{2}{x}$．
∵A點的橫坐標為-1，
∴當x=-1時，y₁=2，
∴A（-1，2）．
∵點A在y₂=ax+1（a≠0）的圖象上，
∴2=-a+1，∴a=-1，
∴一次函數的表達式為y₂=-x+1；

（2）解方程組$\left\{\begin{array}{l}{y=-\frac{2}{x}}\\{y=-x+1}\end{array}\right.$，
得$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$，
∴點B的坐標為（2，-1）．
觀察圖象可知，當x＜-1或0＜x＜2時，
反比例函數y₁的值小于一次函數y₂的值．

點評 本題主要考查了反比例函數系數k的幾何意義、運用待定系數法求一次函數的表達式、反比例函數與一次函數的圖象的交點坐標等知識，運用數形結合的思想是解決第（2）小題的關鍵．