
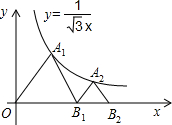 如圖,△OA1B1,△B1A2B2是等邊三角形,點A1,A2在函數y=
如圖,△OA1B1,△B1A2B2是等邊三角形,點A1,A2在函數y=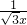 的圖象上,點B1,B2在x軸的正半軸上,分別求△OA1B1,△B1A2B2的面積.
的圖象上,點B1,B2在x軸的正半軸上,分別求△OA1B1,△B1A2B2的面積.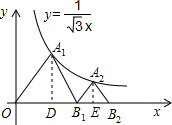 解:分別過A1、A2作x軸的垂線,垂足分別為D、E,如圖,
解:分別過A1、A2作x軸的垂線,垂足分別為D、E,如圖, OD=
OD= m,A2E=
m,A2E= B1E=
B1E= n,OE=2m+n,
n,OE=2m+n, m),A2的坐標為(2m+n,
m),A2的坐標為(2m+n, n),
n),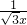 的圖象上,
的圖象上, m=
m= ,解得m=
,解得m= (m=-
(m=- 舍去),
舍去), ,OE=
,OE= +n.
+n.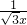 的圖象上,
的圖象上, n•(
n•( +n)=
+n)= ,解得n1=
,解得n1=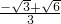 ,n2=
,n2=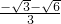 (舍去),
(舍去),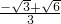 ,
,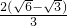 ,
, OB12=
OB12= ×(
×( )2=
)2= ,
, B1B22=
B1B22= ×[
×[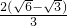 ]2=
]2=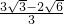 .
. OD=
OD= m,A2E=
m,A2E= B1E=
B1E= n,OE=2m+n,得到A1的坐標為(m,
n,OE=2m+n,得到A1的坐標為(m, m),A2的坐標為(2m+n,
m),A2的坐標為(2m+n, n),然后先把A1的坐標代入反比例解析式求得m的值,再把A2的坐標代入反比例解析式得到n的值,這樣就確定兩等邊三角形的邊長,然后根據等邊三角形的面積等于其邊長的平方的
n),然后先把A1的坐標代入反比例解析式求得m的值,再把A2的坐標代入反比例解析式得到n的值,這樣就確定兩等邊三角形的邊長,然后根據等邊三角形的面積等于其邊長的平方的 倍計算即可.
倍計算即可.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
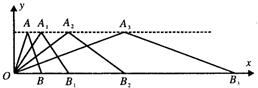 23、如圖,在直角坐標系中,第一次將△OAB變換成△OA1B1,第二次將△OA1B1變換成△OA2B2,第三次將△OA2B2變換成△OA3B3…
23、如圖,在直角坐標系中,第一次將△OAB變換成△OA1B1,第二次將△OA1B1變換成△OA2B2,第三次將△OA2B2變換成△OA3B3…查看答案和解析>>
科目:初中數學 來源: 題型:
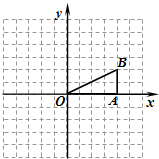 19、如圖,網格小正方形的邊長為1,△OAB為格點三角形(頂點都是格點),以O為坐標原點,OA所在直線為x軸建立平面直角坐標系.將△OAB繞點O按逆時針方向旋轉90°得到△OA1B1.
19、如圖,網格小正方形的邊長為1,△OAB為格點三角形(頂點都是格點),以O為坐標原點,OA所在直線為x軸建立平面直角坐標系.將△OAB繞點O按逆時針方向旋轉90°得到△OA1B1.查看答案和解析>>
科目:初中數學 來源: 題型:
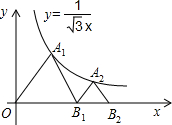 如圖,△OA1B1,△B1A2B2是等邊三角形,點A1,A2在函數y=
如圖,△OA1B1,△B1A2B2是等邊三角形,點A1,A2在函數y=| 1 | ||
|
查看答案和解析>>
科目:初中數學 來源:2008年浙江省寧波市余姚中學自主招生考試數學試卷(解析版) 題型:解答題
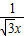 的圖象上,點B1,B2在x軸的正半軸上,分別求△OA1B1,△B1A2B2的面積.
的圖象上,點B1,B2在x軸的正半軸上,分別求△OA1B1,△B1A2B2的面積.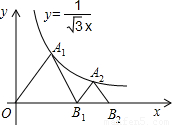
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com