
如圖2,在一張矩形紙片ABCD中,AB=4,BC=8,點E,F分別在AD,BC上,將紙片ABCD沿直線EF折疊,點C落在AD上的一點H處,點D落在點G處,下列結論:①四邊形CFHE是菱形;②EC平分∠DCH;③線段BF的取值范圍為3≤BF≤4;④當點H與點A重合時,EF=2 .其中結論正確的個數是( ).
.其中結論正確的個數是( ).

(A)1個 (B)2個 (C)3個 (D)4個
C
【解析】
試題分析:先判斷出四邊形CFHE是平行四邊形,再根據翻折的性質可得CF=FH,然后根據鄰邊相等的平行四邊形是菱形證明,判斷出①正確;根據菱形的對角線平分一組對角線可得∠BCH=∠ECH,然后求出只有∠DCE=30°時EC平分∠DCH,判斷出②錯誤;點H與點A重合時,設BF=x,表示出AF=FC=8-x,利用勾股定理列出方程求解得到BF的最小值,點G與點D重合時,CF=CD,求出BF=4,然后寫出BF的取值范圍,判斷出③正確;過點F作FM⊥AD于M,求出ME,再利用勾股定理列式求解得到EF,判斷出④正確.
∵FH與CG,EH與CF都是矩形ABCD的對邊AD、BC的一部分,
∴FH∥CG,EH∥CF,
∴四邊形CFHE是平行四邊形,
由翻折的性質得,CF=FH,
∴四邊形CFHE是菱形,(故①正確);
∴∠BCH=∠ECH,
∴只有∠DCE=30°時EC平分∠DCH,(故②錯誤);
點H與點A重合時,設BF=x,則AF=FC=8-x,
在Rt△ABF中,AB2+BF2=AF2,
即42+x2=(8-x)2,
解得x=3,
點G與點D重合時,CF=CD=4,
∴BF=4,
∴線段BF的取值范圍為3≤BF≤4,(故③正確);
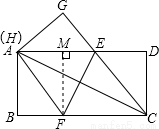
過點F作FM⊥AD于M,
則ME=(8-3)-3=2,
由勾股定理得,
EF=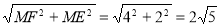 ,(故④正確);
,(故④正確);
綜上所述,結論正確的有①③④共3個.
故選:C.
考點:1.翻折變換(折疊問題);2.勾股定理的應用;3.菱形的判定與性質.


 互動課堂系列答案
互動課堂系列答案 激活思維智能訓練課時導學練系列答案
激活思維智能訓練課時導學練系列答案科目:初中數學 來源:2014-2015學年廣東省汕頭市七年級上學期期中考試數學試卷(解析版) 題型:選擇題
下列是一元一次方程的是( )
A、x+2y=1 B、t2+t-1=0 C、5y-3 D、4x=8
查看答案和解析>>
科目:初中數學 來源:2014-2015學年廣東省廣州市九年級上學期期中考試數學試卷(解析版) 題型:填空題
Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C為圓心,r為半徑作圓,若圓C與直線AB相切,則r的值為_________cm
查看答案和解析>>
科目:初中數學 來源:2014-2015學年廣東省廣州市九年級上學期綜合測試一數學試卷(解析版) 題型:解答題
某校為美化校園,計劃對面積為1800m2的區域進行綠化,安排甲、乙兩個工程隊完成.已知甲隊每天能完成綠化的面積是乙隊每天能完成綠化的面積的2倍,并且在獨立完成面積為400m2區域的綠化時,甲隊比乙隊少用4天.
(1)求甲、乙兩工程隊每天能完成綠化的面積分別是多少m2?
(2)若學校每天需付給甲隊的綠化費用為0.4萬元,乙隊為0.25萬元,要使這次的綠化總費用不超過8萬元,至少應安排甲隊工作多少天?
查看答案和解析>>
科目:初中數學 來源:2014-2015學年廣東省廣州市九年級上學期綜合測試一數學試卷(解析版) 題型:填空題
已知線段CD是由線段AB平移得到的,點A(﹣1,4)的對應點為C(4,7),則點B(﹣4,﹣1)的對應點D的坐標為 .
查看答案和解析>>
科目:初中數學 來源:2014-2015學年廣東省廣州市九年級上學期綜合測試一數學試卷(解析版) 題型:選擇題
我市7月的某一周每天的最高氣溫(單位:℃)統計如下:34,36,35,36,36,35,33,則這組數據的中位數與眾數分別是( ).
(A)35,35 (B)36,36 (C)35,36 (D)36,35
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省江陰市長涇片九年級上學期期中考試數學試卷(解析版) 題型:解答題
(本題滿分6分)已知關于 的一元二次方程
的一元二次方程 有兩個實數根
有兩個實數根 和
和 .
.
(1)求實數 的取值范圍;
的取值范圍;
(2)當 時,求
時,求 的值.
的值.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省江陰市長涇片七年級上學期期中考試數學試卷(解析版) 題型:選擇題
若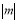 =3,
=3, =5且m-n>0,則m+n的值是 ( )
=5且m-n>0,則m+n的值是 ( )
A.-2 B.-8或 -2 C.-8或 8 D.8或-2
查看答案和解析>>
科目:初中數學 來源: 題型:單選題
如圖,若將直尺的0cm刻度與半徑為5cm的量角器的0°對齊,并讓量角器沿直尺的邊緣無滑動滾動,則直尺上的10cm刻度對應的量角器上的度數大約為
| A.95° | B.115° | C.125° | D.180° |

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com