
 如圖,AB為⊙O的直徑,C為⊙O上一點,AD和過C點的直線互相垂直,垂足為D,且AC平分∠DAB.
如圖,AB為⊙O的直徑,C為⊙O上一點,AD和過C點的直線互相垂直,垂足為D,且AC平分∠DAB.分析 (1)連接OC,由等腰三角形的性質和角平分線的定義得出∠DAC=∠OCA,于是可判斷OC∥AD,由于AD⊥CD,則OC⊥CD,然后根據切線的判定定理即可得到結論;
(2)連接BC,根據圓周角定理得到∠ACB=90°,由于∠DAC=∠OAC,則可判斷△ACD∽△ABC,然后利用相似比可計算出CD的長.
解答 (1)證明:連接OC.如圖1所示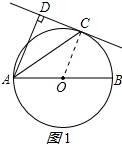
∵AC平分∠DAB,
∴∠DAC=∠OAC,
∵OA=OC,
∴∠OCA=∠OAC,
∴∠DAC=∠OCA,
∴DA∥OC,
∵AD⊥DC,
∴∠ADC=90°,
∴∠OCD=90°,
即OC⊥DC,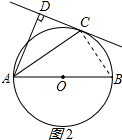
∵OC為半徑,
∴DC為⊙O的切線.
(2)解:連接BC,如圖2所示:
∵AB是⊙O的直徑,
∴AB=10,∠ACB=90°=∠ADC,
∴AC=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
又∵∠DAC=∠OAC,
∴△ACD∽△ABC,
∴$\frac{CD}{BC}=\frac{AC}{AB}$,即$\frac{CD}{6}=\frac{8}{10}$,
解得:CD=4.8.
點評 本題考查了切線的判定、等腰三角形的性質、平行線的判定與性質、圓周角定理、勾股定理、相似三角形的判定與性質;熟練掌握切線的判定,由圓周角定理證出△ACD∽△ABC是解決問題(2)的關鍵.


科目:初中數學 來源: 題型:解答題
 如圖,利用一面墻,用長80m的籬笆圍成一個矩形場地,能否使所圍矩形場地的面積超過800m2?如果能,請求出BC的長,如果不能,請說明理由.
如圖,利用一面墻,用長80m的籬笆圍成一個矩形場地,能否使所圍矩形場地的面積超過800m2?如果能,請求出BC的長,如果不能,請說明理由.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知A(1,-3),B(-2,-2),C(2,0).
如圖,已知A(1,-3),B(-2,-2),C(2,0).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
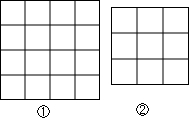 如圖,每個小正方形的邊長都是1,每個小格的頂點叫做格點,以格點為頂點,分別按下列要求畫三角形:
如圖,每個小正方形的邊長都是1,每個小格的頂點叫做格點,以格點為頂點,分別按下列要求畫三角形:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 3 | B. | 5 | C. | 7 | D. | 9 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com