
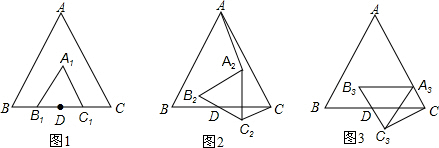
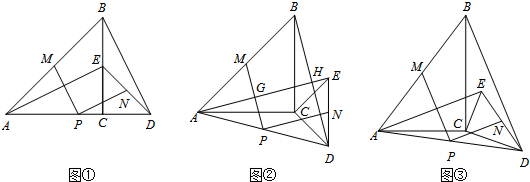
 已知,△ABC和△A1B1C1均為正三角形,BC和B1C1的中點均為D,如圖1.
已知,△ABC和△A1B1C1均為正三角形,BC和B1C1的中點均為D,如圖1.分析 (1)利用等邊三角形的性質以及結合相似三角形的判定與性質得出得∠A2AD=∠C2CD,進而得出∠ADE=∠CFE=90°,即可得出答案;
(2)首先連接A3D,過C3作C3G⊥BC于G,進而得出C3C,C3G的長,進而利用多邊形ABDC3C的面積=S△ABC+S△CC3D,求出答案.
解答 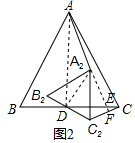 解:(1)AA2⊥CC2
解:(1)AA2⊥CC2
理由:在圖2中,連接AD、A2D、延長AA2交BC于E,交CC2于F,
∵BC和B1C1的中點均為D,△A1B1C1繞點D旋轉到△A2B2C2,
∴∠ADA2=90°-∠A2DC=∠CDC2,$\frac{AD}{{D{A_2}}}=\frac{DC}{{D{C_2}}}$,(等邊三角形都相似,相似三角形對應高的比等于相似比),
∴△AA2D∽△CC2D,
于是得∠A2AD=∠C2CD,
又∵∠AED=∠CEF,
∴∠ADE=∠CFE=90°,
∴AA2⊥CC2;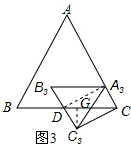
(2)在圖3中,連接A3D,過C3作C3G⊥BC于G,由(1)得AC⊥CC3,
由題意得A3D⊥AC,四邊形A3CC3D是矩形,
則C3C=A3D=2sin60°=$\sqrt{3}$,
C3G=$\sqrt{3}$sin(90°-60°)=$\frac{\sqrt{3}}{2}$,
故多邊形ABDC3C的面積=S△ABC+S△CC3D=$\frac{1}{2}$×4×4sin60°+$\frac{1}{2}$×2×$\frac{\sqrt{3}}{2}$=$\frac{{9\sqrt{3}}}{2}$.
點評 此題主要考查了幾何變換以及相似三角形的判定與性質和解直角三角形的應用,正確利用相似三角形的判定與性質是解題關鍵.


科目:初中數學 來源: 題型:填空題
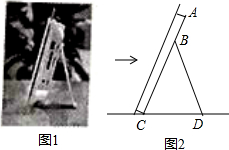 如圖1是小紅同學書桌上的一個電子相框,將其側面抽象為如圖2所示的幾何圖形,已知BC=BD=18cm,∠CBD=40°,則點B到CD的距離為16.9cm(用科學計算器計算.參考數據sin20°≈0.342,cos20°≈0.940,sin40°≈0.643,cos40°≈0.766,結果精確到0.1cm).
如圖1是小紅同學書桌上的一個電子相框,將其側面抽象為如圖2所示的幾何圖形,已知BC=BD=18cm,∠CBD=40°,則點B到CD的距離為16.9cm(用科學計算器計算.參考數據sin20°≈0.342,cos20°≈0.940,sin40°≈0.643,cos40°≈0.766,結果精確到0.1cm).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
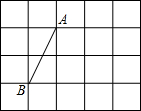 如圖,A、B兩點均在由小正方形組成的網格格點上,若C點也在格點上,且△ABC是等腰直角三角形,則符合條件的C點的個數有( )
如圖,A、B兩點均在由小正方形組成的網格格點上,若C點也在格點上,且△ABC是等腰直角三角形,則符合條件的C點的個數有( )| A. | 3個 | B. | 4個 | C. | 5個 | D. | 6個 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 鈍角三角形 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 矩形一邊長/m | 5 | 10 | 15 | 20 |
| 矩形面積/m2 | 125 | 200 | 225 | 200 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com