
【題目】如圖,![]() 是矩形
是矩形![]() 的對角線的交點,
的對角線的交點,![]() 、
、![]() 、
、![]() 、
、![]() 分別是
分別是![]() 、
、![]() 、
、![]() 、
、![]() 上的點,且
上的點,且![]() .
.

![]() 求證:四邊形
求證:四邊形![]() 是矩形;
是矩形;
![]() 若
若![]() 、
、![]() 、
、![]() 、
、![]() 分別是
分別是![]() 、
、![]() 、
、![]() 、
、![]() 的中點,且
的中點,且![]() ,
,![]() ,求矩形
,求矩形![]() 的面積.
的面積.
【答案】(1)證明見解析;(2)![]()
【解析】
(1)首先證明四邊形EFGH是平行四邊形,然后再證明HF=EG;
(2)根據已知求出矩形的邊長CD和BC,然后根據矩形面積公式即可求得結論.
(1)∵四邊形ABCD是矩形,∴OA=OB=OC=OD.
∵AE=BF=CG=DH,∴OE=OF=OG=OH,∴四邊形EFGH是矩形;
(2)∵G是OC的中點,∴GO=GC.
∵DG⊥AC,∴∠DGO=∠DGC=90°.
又∵DG=DG,∴△DGC≌△DGO,∴CD=OD.
∵F是BO中點,OF=2cm,∴BO=4cm.
∵四邊形ABCD是矩形,∴DO=BO=4cm,∴DC=4cm,DB=8cm,∴CB=![]() =4
=4![]() ,∴矩形ABCD的面積=4×4
,∴矩形ABCD的面積=4×4![]() =16
=16![]() cm2.
cm2.


科目:初中數學 來源: 題型:
【題目】操作:在![]() 中,
中,![]() ,
,![]() ,將一塊等腰直角三角板的直角頂點放在斜邊
,將一塊等腰直角三角板的直角頂點放在斜邊![]() 的中點
的中點![]() 處,將三角板繞點
處,將三角板繞點![]() 旋轉,三角板的兩直角邊分別交射線
旋轉,三角板的兩直角邊分別交射線![]() 、
、![]() 于
于![]() 、
、![]() 兩點.圖
兩點.圖![]() ,
,![]() ,
,![]() 是旋轉三角板得到的圖形中的
是旋轉三角板得到的圖形中的![]() 種情況.
種情況.
研究:
![]() 三角板繞點
三角板繞點![]() 旋轉,觀察線段
旋轉,觀察線段![]() 和
和![]() 之間有什么數量關系,并結合圖
之間有什么數量關系,并結合圖![]() 加以證明;
加以證明;
![]() 三角板繞點
三角板繞點![]() 旋轉,
旋轉,![]() 是否能成為等腰三角形?若能,指出所有情況(即寫出
是否能成為等腰三角形?若能,指出所有情況(即寫出![]() 為等腰三角形時
為等腰三角形時![]() 的長);若不能,請說明理由;
的長);若不能,請說明理由;
![]() 若將三角板的直角頂點放在斜邊
若將三角板的直角頂點放在斜邊![]() 上的
上的![]() 處,且
處,且![]() ,和前面一樣操作,試問線段
,和前面一樣操作,試問線段![]() 和
和![]() 之間有什么數量關系?并結合圖
之間有什么數量關系?并結合圖![]() 加以證明.
加以證明.




查看答案和解析>>
科目:初中數學 來源: 題型:
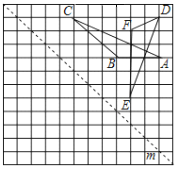
【題目】如圖,在由邊長均為1個單位長度的小正方形組成的網格中,給出了格點△ABC和△DEF(頂點 為網格線的交點),以及經過格點的直線m.
(1)畫出△ABC關于直線m對稱的△A1B1C1;
(2)將△DEF先向左平移5個單位長度,再向下平移4個單位長度,畫出平移后得到的△D1E1F1;
(3)求∠A+∠E= ________°.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分別找一點M、N,使△AMN周長最小,此時∠MAN的度數為_________°.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com