
 ,連結DE,過點B作BP平行于DE,交⊙O于點P,連結EP、CP、OP.
,連結DE,過點B作BP平行于DE,交⊙O于點P,連結EP、CP、OP.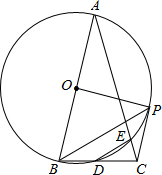

 。
。 (180°-30°)=75°。∴∠DEC=75°。
(180°-30°)=75°。∴∠DEC=75°。 。
。 ,∴
,∴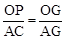 。∴
。∴ 。
。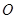 的切線。
的切線。 ,從而可得出BD=DE,故BD=DE=DC,所以∠DEC=∠DCE,△ABC中由等腰三角形的性質可得出∠ABC=75°,故∠DEC=75°由三角形內角和定理得出∠EDC的度數,再根據BP∥DE可知∠PBC=∠EDC=30°,進而得出∠ABP的度數,再由OB=OP,可知∠OBP=∠OPB,由三角形內角和定理即可得出∠BOP=90°。
,從而可得出BD=DE,故BD=DE=DC,所以∠DEC=∠DCE,△ABC中由等腰三角形的性質可得出∠ABC=75°,故∠DEC=75°由三角形內角和定理得出∠EDC的度數,再根據BP∥DE可知∠PBC=∠EDC=30°,進而得出∠ABP的度數,再由OB=OP,可知∠OBP=∠OPB,由三角形內角和定理即可得出∠BOP=90°。 ,由
,由 得
得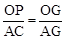 ,
, ,由∠AGO=∠CGP可得出△AOG∽△CPG,由相似三角形形的性質可知∠GPC=∠AOG=90°,故可得出CP是⊙O的切線。
,由∠AGO=∠CGP可得出△AOG∽△CPG,由相似三角形形的性質可知∠GPC=∠AOG=90°,故可得出CP是⊙O的切線。 

科目:初中數學 來源:不詳 題型:解答題
 的半徑
的半徑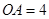 ,
,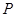 是
是 延長線上一點,過線段
延長線上一點,過線段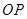 的中點
的中點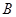 作垂線交
作垂線交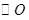 于點
于點 ,射線
,射線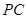 交
交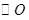 于點
于點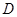 ,聯結
,聯結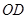 .
.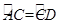 ,求弦
,求弦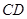 的長.
的長. 在
在 上時,設
上時,設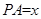 ,
, ,求
,求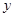 與
與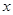 的函數關系式及自變量
的函數關系式及自變量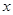 的取值范圍;
的取值范圍;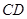 的中點為
的中點為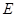 ,射線
,射線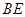 與射線
與射線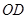 交于點
交于點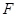 ,當
,當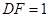 時,請直接寫出
時,請直接寫出 的值.
的值.
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
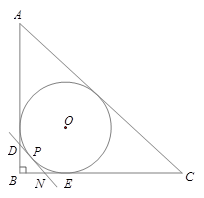
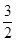 r C.2r D.
r C.2r D. 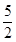 r
r查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題
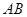 繞它的中點
繞它的中點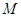 ,按逆時針方向旋轉30°,則線段
,按逆時針方向旋轉30°,則線段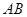 掃過的面積為 .
掃過的面積為 .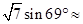 (精確到0.01).
(精確到0.01).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com