
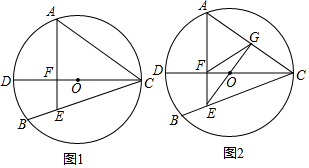
分析 (1)連接AD,根據同角的余角相等得:∠ADF=∠FAC,再由同圓中弦相等,則弧相等,進而由等弧所對的圓周角相等得:∠ADF=∠ACB,所以∠FAC=∠ACB;
(2)作輔助線,先證明△AOE≌△COE,得∠AEO=∠CEO,由等腰三角形三線合一的性質得:G是AC的中點,再根據直角三角形斜邊的中線等于斜邊一半可得結論:AC=2FG;
(3)如圖3,作輔助線,構建高線GH和中位線,證明F、E、C、G四點共圓,則tan∠FGE=tan∠FCE=$\frac{\sqrt{2}}{4}$,EF=$\sqrt{2}$a,FC=4a,利用勾股定理得:EC和AC的長,根據四邊形FECG的面積為14$\sqrt{2}$,列式可得結論.
解答 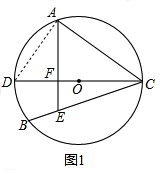 證明:(1)如圖1,連接AD,
證明:(1)如圖1,連接AD,
∵DC為⊙O的直徑,
∴∠DAC=90°,
∵AF⊥CD,
∴∠AFD=90°,
∴∠ADF+∠DAF=∠FAC+∠DAF,
∴∠ADF=∠FAC,
∵AB=AC,
∴$\widehat{AB}$=$\widehat{AC}$,
∴∠ADF=∠ACB,
∴∠FAC=∠ACB;
(2)連接AO,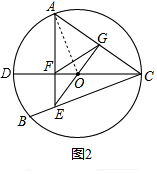
∵AO=OC,
∴∠OAC=∠OCA,
∵∠CAF=∠ACB,
∴∠EAO=∠ECO,AE=EC,
∴△AOE≌△COE,
∴∠AEO=∠CEO,
∴EG平分∠AEC,
∵△AEC是等腰三角形,
∴G是AC的中點,
∵△AFC是直角三角形,
∴AC=2FG;
(3)如圖3,過G作GH⊥DC于H,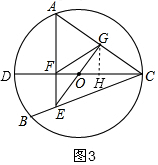
∵AF⊥CD,
∴AF∥GH,
在Rt△AFC中,
∵G是AC的中點,
∴AG=CG,GH=$\frac{1}{2}$AF,
∴∠EAC=∠AFG,
∵∠EAC=∠ECA,
∴∠AFG=∠ECA,
∵∠AFG+∠EFG=180°,
∴∠ECA+∠EFG=180°,
∴F、E、C、G四點共圓,
∴∠FGE=∠FCE,
∵tan∠FGE=$\frac{\sqrt{2}}{4}$,
∴tan∠FCE=$\frac{\sqrt{2}}{4}$,
即$\frac{FE}{FC}=\frac{\sqrt{2}}{4}$,
設EF=$\sqrt{2}$a,FC=4a,
由勾股定理得:EC=$\sqrt{(\sqrt{2}a)^{2}+(4a)^{2}}$=3$\sqrt{2}$a,
∵AE=EC=3$\sqrt{2}$a,
∴AF=AE-EF=3$\sqrt{2}$a-$\sqrt{2}$a=2$\sqrt{2}$a,
∴GH=$\sqrt{2}$a,
由勾股定理得:AC=$\sqrt{(2\sqrt{2}a)^{2}+(4a)^{2}}$=2$\sqrt{6}$a,
∵四邊形FECG的面積為14$\sqrt{2}$,
則S△EFC+S△FCG=14$\sqrt{2}$,
∴$\frac{1}{2}$EF•FC+$\frac{1}{2}$FC•GH=14$\sqrt{2}$,
∴$\frac{1}{2}$×$\sqrt{2}$a×4a+$\frac{1}{2}$×4a×$\sqrt{2}$a=14$\sqrt{2}$,
∴a=$\frac{\sqrt{14}}{2}$,
∴AC=2$\sqrt{6}$a=2$\sqrt{6}$×$\frac{\sqrt{14}}{2}$=$\sqrt{84}$=2$\sqrt{21}$.
點評 本題是圓的綜合題,考查了四點共圓的性質和判定、三角函數、圓周角定理、三角形全等的性質和判定、勾股定理等知識,第三問中利用四點共圓將∠FGE轉化為∠FCE是關鍵,根據正切比的關系設未知數,由已知等量關系列方程可得出結果.


 新思維假期作業寒假吉林大學出版社系列答案
新思維假期作業寒假吉林大學出版社系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,在平面直角坐標系中,第一次將△OAB變換成△OA1B1,第二次將△OA1B1變換成△OA2B2,第三次將△OA2B2變換成△OA3B3.已知A(1,3),A1(2,3),A2(4,3),A3 (8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).
如圖,在平面直角坐標系中,第一次將△OAB變換成△OA1B1,第二次將△OA1B1變換成△OA2B2,第三次將△OA2B2變換成△OA3B3.已知A(1,3),A1(2,3),A2(4,3),A3 (8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
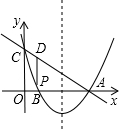 如圖,拋物線y=x2+bx+c過點A(3,0),B(1,0),交y軸于點C,點P是該拋物線上一動點,點P從點C沿拋物線向A點運動(運動到A點停止),過點P作PD∥y軸交直線AC于點D.
如圖,拋物線y=x2+bx+c過點A(3,0),B(1,0),交y軸于點C,點P是該拋物線上一動點,點P從點C沿拋物線向A點運動(運動到A點停止),過點P作PD∥y軸交直線AC于點D.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
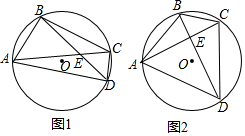 已知:⊙O是四邊形ABCD的外接圓,AC與BD交于點E.
已知:⊙O是四邊形ABCD的外接圓,AC與BD交于點E.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com