
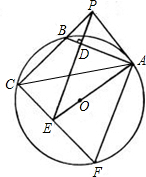
 連接CE并延長,交⊙O于F,連接AF.
連接CE并延長,交⊙O于F,連接AF. ,AB=2,求EF的長.
,AB=2,求EF的長. =cos∠APE=
=cos∠APE=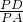 .
.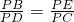 ,
, =
=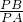 …①,
…①,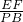 =
=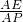 ,即
,即 =
=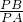 …②
…② =
= ,
, =
= ×2=
×2= .
. =
= ,再代值即可求出EF的長.
,再代值即可求出EF的長.

科目:初中數學 來源: 題型:
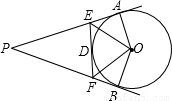
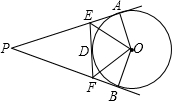 如圖,已知:PA、PB、EF 分別切⊙O 于A、B、D,若PA=10cm,那么△PEF 周長是
如圖,已知:PA、PB、EF 分別切⊙O 于A、B、D,若PA=10cm,那么△PEF 周長是查看答案和解析>>
科目:初中數學 來源: 題型:
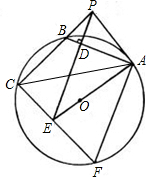 連接CE并延長,交⊙O于F,連接AF.
連接CE并延長,交⊙O于F,連接AF.| 2 |
查看答案和解析>>
科目:初中數學 來源:2010年四川省成都市實驗外國語學校直升考試數學模擬試卷(解析版) 題型:解答題
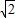 ,AB=2,求EF的長.
,AB=2,求EF的長.
查看答案和解析>>
科目:初中數學 來源:2010年天津一中中考數學模擬試卷(解析版) 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com