
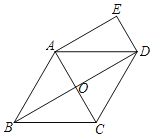
【題目】已知:如圖,在菱形ABCD中,對角線AC、BD相交于點O,DE∥AC,AE∥BD.
(1)求證:四邊形AODE是矩形;
(2)若AB=2,∠BCD=120°,求四邊形AODE的面積.
【答案】(1)見解析;(2)![]()
【解析】
(1)根據菱形的性質得出AC⊥BD,再根據平行四邊形的判定定理得四邊形AODE為平行四邊形,由矩形的判定定理得出四邊形AODE是矩形;
(2)證明△ABC是等邊三角形,得出OA=1,由勾股定理得出OB=![]() ,由菱形的性質得出OD=OB=
,由菱形的性質得出OD=OB=![]() ,即可求出四邊形AODE的面積.
,即可求出四邊形AODE的面積.
(1)證明:∵DE∥AC,AE∥BD,
∴四邊形AODE是平行四邊形,
∵在菱形ABCD中,AC⊥BD,
∴∠AOD=90°,
∴四邊形AODE是矩形;
(2)解:∵∠BCD=120°,AB∥CD,
∴∠ABC=180°﹣120°=60°,
∵AB=BC=2,
∴△ABC是等邊三角形,
∴OA=![]() ×2=1,
×2=1,
∵在菱形ABCD中,AC⊥BD
∴由勾股定理OB=![]() ,
,
∵四邊形ABCD是菱形,
∴OD=OB=![]() ,
,
∴四邊形AODE的面積=OAOD=![]() .
.


 時刻準備著暑假作業原子能出版社系列答案
時刻準備著暑假作業原子能出版社系列答案科目:初中數學 來源: 題型:
【題目】根據以下信息,解答下列問題.

(1)小華同學設乙型機器人每小時搬運xkg產品,可列方程為 .
小惠同學設甲型機器人搬運800kg所用時間為y小時,可列方程為 .
(2)請你按照(1)中小華同學的解題思路,寫出完整的解答過程.
查看答案和解析>>
科目:初中數學 來源: 題型:
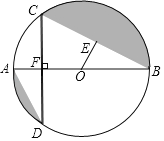
【題目】如圖,AB為⊙O直徑,OE⊥BC垂足為E,AB⊥CD垂足為F.
(1)求證:AD=2OE;
(2)若∠ABC=30°,⊙O的半徑為2,求兩陰影部分面積的和.
查看答案和解析>>
科目:初中數學 來源: 題型:
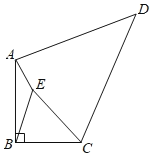
【題目】如圖,在四邊形ABCD中,∠B=90°,∠D=45°,AB=BC=2,點E為四邊形ABCD內部一點,且滿足CE2﹣AE2=2BE2,則點E在運動過程中所形成的圖形的長為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
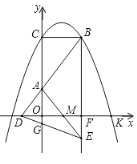
【題目】如圖,![]() 與
與![]() 軸交于點C,與
軸交于點C,與![]() 軸的正半軸交于點K,過點
軸的正半軸交于點K,過點![]() 作
作![]() 軸交拋物線于另一點B,點
軸交拋物線于另一點B,點![]() 在
在![]() 軸的負半軸上,連結
軸的負半軸上,連結![]() 交
交![]() 軸于點A,若
軸于點A,若![]() .
.
(1)用含![]() 的代數式表示
的代數式表示![]() 的長;
的長;
(2)當![]() 時,判斷點
時,判斷點![]() 是否落在拋物線上,并說明理由;
是否落在拋物線上,并說明理由;
(3)過點![]() 作
作![]() 軸交
軸交![]() 軸于點
軸于點![]() 延長
延長![]() 至
至![]() ,使得
,使得![]() 連結
連結![]() 交
交![]() 軸于點
軸于點![]() 連結AE交
連結AE交![]() 軸于點
軸于點![]() 若
若![]() 的面積與
的面積與![]() 的面積之比為
的面積之比為![]() 則求出拋物線的解析式.
則求出拋物線的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在正方形 ABCD 中, P 為 AB 的中點,![]() 的延長線于點 E ,連接 AE 、 BE ,
的延長線于點 E ,連接 AE 、 BE ,![]() 交 DP 于點 F ,連接 BF 、FC ,下列結論:①
交 DP 于點 F ,連接 BF 、FC ,下列結論:① ![]() ;② FB AB ;③
;② FB AB ;③ ![]() ;④ FC EF . 其中正確的是( )
;④ FC EF . 其中正確的是( )
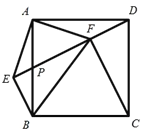
A.①②④B.①③④C.①②③D.①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,DC∥AB,DA⊥AB,AD=4cm,DC=5cm,AB=8cm.如果點P由B點出發沿BC方向向點C勻速運動,同時點Q由A點出發沿AB方向向點B勻速運動,它們的速度均為1cm/s,當P點到達C點時,兩點同時停止運動,連接PQ,設運動時間為t s,解答下列問題:
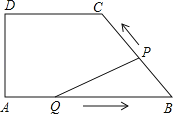
(1)當t為何值時,P,Q兩點同時停止運動;
(2)設△PQB的面積為S,當t為何值時,S取得最大值,并求出最大值;
(3)當△PQB為等腰三角形時,求t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知C為線段AB中點,∠ACM=α.Q為線段BC上一動點(不與點B重合),點P在射線CM上,連接PA,PQ,記BQ=kCP.
(1)若α=60°,k=1,
①如圖1,當Q為BC中點時,求∠PAC的度數;
②直接寫出PA、PQ的數量關系;
(2)如圖2,當α=45°時.探究是否存在常數k,使得②中的結論仍成立?若存在,寫出k的值并證明;若不存在,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com