
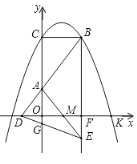
【題目】如圖,![]() 與
與![]() 軸交于點C,與
軸交于點C,與![]() 軸的正半軸交于點K,過點
軸的正半軸交于點K,過點![]() 作
作![]() 軸交拋物線于另一點B,點
軸交拋物線于另一點B,點![]() 在
在![]() 軸的負(fù)半軸上,連結(jié)
軸的負(fù)半軸上,連結(jié)![]() 交
交![]() 軸于點A,若
軸于點A,若![]() .
.
(1)用含![]() 的代數(shù)式表示
的代數(shù)式表示![]() 的長;
的長;
(2)當(dāng)![]() 時,判斷點
時,判斷點![]() 是否落在拋物線上,并說明理由;
是否落在拋物線上,并說明理由;
(3)過點![]() 作
作![]() 軸交
軸交![]() 軸于點
軸于點![]() 延長
延長![]() 至
至![]() ,使得
,使得![]() 連結(jié)
連結(jié)![]() 交
交![]() 軸于點
軸于點![]() 連結(jié)AE交
連結(jié)AE交![]() 軸于點
軸于點![]() 若
若![]() 的面積與
的面積與![]() 的面積之比為
的面積之比為![]() 則求出拋物線的解析式.
則求出拋物線的解析式.
【答案】(1)BC=m;(2)點D在拋物線上,理由見解析; (3)![]() .
.
【解析】
(1)先求出拋物線的對稱軸,然后根據(jù)點C與點B關(guān)于對稱軸對稱即可求出BC的長;
(2)根據(jù)題意即可求出BC和二次函數(shù)解析式,根據(jù)利用平行證出△AOD∽△ACB,列出比例式即可求出點D的坐標(biāo),最后代入解析式即可判斷結(jié)論;
(3)根據(jù)已知條件可得點E的坐標(biāo)為(m,![]() ),即OF=m,EF=
),即OF=m,EF=![]() ,△ODG∽△FDE,然后用m表示出OD、DF、OG、MF和OM,再利用平行證出△AOM∽△EFM,列出比例式即可求出m的值,從而求出結(jié)論.
,△ODG∽△FDE,然后用m表示出OD、DF、OG、MF和OM,再利用平行證出△AOM∽△EFM,列出比例式即可求出m的值,從而求出結(jié)論.
解:(1)![]() 圖象的對稱軸為直線x=
圖象的對稱軸為直線x=![]() ,點C與點B關(guān)于對稱軸對稱
,點C與點B關(guān)于對稱軸對稱
∴BC=![]() =m;
=m;
(2)在,理由如下
當(dāng)m=2時,BC=2,![]()
∵![]() ,
,![]()
∴△AOD∽△ACB
∴![]()
∴OD=![]() BC=1
BC=1
∴點D的坐標(biāo)為(-1,0)
當(dāng)x=-1時,![]()
∴點D在拋物線.
(3)∵![]() ,
,![]()
∴點E的坐標(biāo)為(m,![]() ),即OF=m,EF=
),即OF=m,EF=![]() ,△ODG∽△FDE
,△ODG∽△FDE
由(2)可知![]()
∴OD=![]() BC=
BC=![]() m,OA=
m,OA=![]() OC
OC
∴DF=OD+OF=![]() m
m
∴![]()
即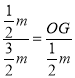
解得:OG=![]() m
m
∵![]() 的面積與
的面積與![]() 的面積之比為
的面積之比為![]()
∴![]() EF·MF=2×
EF·MF=2×![]() OD·OG
OD·OG
即![]() ·
·![]() ·MF=2×
·MF=2×![]() ·
·![]() m·
m·![]() m
m
解得:MF=![]() m
m
∴OM=OF-MF=![]() m
m
將x=0代入![]() 中,解得y=3
中,解得y=3
∴OC=3
∴OA=1
∵OA∥EF
∴△AOM∽△EFM
∴![]()
即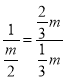
解得:m=1
∴拋物線的解析式為![]()


科目:初中數(shù)學(xué) 來源: 題型:
【題目】受國內(nèi)外復(fù)雜多變的經(jīng)濟(jì)環(huán)境影響,去年1至7月,原材料價格一路攀升,長沙市某服裝廠每件衣服原材料的成本y1(元)與月份x(1≤x≤7,且x為整數(shù))之間的函數(shù)關(guān)系如下表:
月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
成本(元/件) | 56 | 58 | 60 | 62 | 64 | 66 | 68 |
8至12月,隨著經(jīng)濟(jì)環(huán)境的好轉(zhuǎn),原材料價格的漲勢趨緩,每件原材料成本y2(元)與月份x的函數(shù)關(guān)系式為y2=x+62(8≤x≤12,且x為整數(shù)).
(1)請觀察表格中的數(shù)據(jù),用學(xué)過的函數(shù)相關(guān)知識求y1與x的函數(shù)關(guān)系式.
(2)若去年該衣服每件的出廠價為100元,生產(chǎn)每件衣服的其他成本為8元,該衣服在1至7月的銷售量p1(萬件)與月份x滿足關(guān)系式p1=0.1x+1.1(1≤x≤7,且x為整數(shù)); 8至12月的銷售量p2(萬件)與月份x滿足關(guān)系式p2=﹣0.1x+3(8≤x≤12,且x為整數(shù)),該廠去年哪個月利潤最大;并求出最大利潤.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】設(shè)等邊三角形的內(nèi)切圓半徑為![]() 外接圓半徑為
外接圓半徑為![]() ,平面內(nèi)任意一點
,平面內(nèi)任意一點![]() 到等邊三角形中心的距離為
到等邊三角形中心的距離為![]() 若滿足
若滿足![]() 則稱點
則稱點![]() 叫做等邊三角形的中心關(guān)聯(lián)點.在平面直角坐標(biāo)系
叫做等邊三角形的中心關(guān)聯(lián)點.在平面直角坐標(biāo)系![]() 中,等邊
中,等邊![]() 的三個頂點的坐標(biāo)分別為
的三個頂點的坐標(biāo)分別為![]() .
.
(1)①等邊![]() 中心的坐標(biāo)為 ;
中心的坐標(biāo)為 ;
②已知點![]() 在
在![]() 中,是等邊
中,是等邊![]() 的中心關(guān)聯(lián)點的是 ;
的中心關(guān)聯(lián)點的是 ;
(2)如圖1,過點![]() 作直線交
作直線交![]() 軸正半軸于
軸正半軸于![]() 使
使![]() .
.
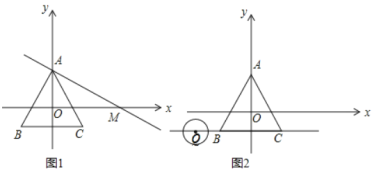
①若線段![]() 上存在等邊
上存在等邊![]() 的中心關(guān)聯(lián)點
的中心關(guān)聯(lián)點![]() 求
求![]() 的取值范圍;
的取值范圍;
②將直線![]() 向下平移得到直線
向下平移得到直線![]() 當(dāng)
當(dāng)![]() 滿足什么條件時,直線
滿足什么條件時,直線![]() 上總存在等邊
上總存在等邊![]() 的中心關(guān)聯(lián)點;
的中心關(guān)聯(lián)點;
(3)如圖2,點![]() 為直線
為直線![]() 上一動點,
上一動點,![]() 的半徑為
的半徑為![]() 當(dāng)
當(dāng)![]() 從點
從點![]() 出發(fā),以每秒
出發(fā),以每秒![]() 個單位的速度向右移動,運動時間為
個單位的速度向右移動,運動時間為![]() 秒.是否存在某一時刻
秒.是否存在某一時刻![]() 使得
使得![]() 上所有點都是等邊
上所有點都是等邊![]() 的中心關(guān)聯(lián)點?如果存在,請直接寫出所有符合題意的
的中心關(guān)聯(lián)點?如果存在,請直接寫出所有符合題意的![]() 的值;如果不存在,請說明理由.
的值;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
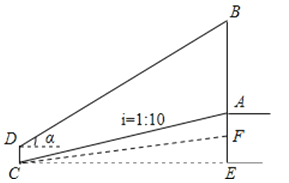
【題目】數(shù)學(xué)活動課上,老師和學(xué)生一起去測量學(xué)校升旗臺上旗桿AB的高度,如圖,老師測得升旗臺前斜坡FC的坡比為iFC=1:10(即EF:CE=1:10),學(xué)生小明站在離升旗臺水平距離為35m(即CE=35m)處的C點,測得旗桿頂端B的仰角為α,已知tanα=![]() ,升旗臺高AF=1m,小明身高CD=1.6m,請幫小明計算出旗桿AB的高度.
,升旗臺高AF=1m,小明身高CD=1.6m,請幫小明計算出旗桿AB的高度.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】家庭過期藥品屬于“危險廢物”,處理不當(dāng)將污染環(huán)境,危害健康某市藥監(jiān)部門為了解家庭處理過期藥品的方式,決定對全市家庭作一次簡單隨機(jī)抽樣調(diào)查.
(1)下列選取樣本的方法最合理的一種是 (只需填上正確答案的序號)
①在市中心某個居民區(qū)以家庭為單位隨機(jī)抽取;
②在全市醫(yī)務(wù)工作者中以家庭為單位隨機(jī)抽取;
③在全市常住人口中以家庭為單位隨機(jī)抽取.
(2)本次抽樣調(diào)查發(fā)現(xiàn),接受調(diào)查的家庭都有過期藥品,現(xiàn)將有關(guān)數(shù)據(jù)呈現(xiàn)如下圖:
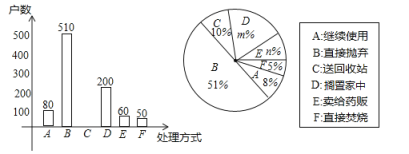
①![]() ,
,
②補(bǔ)全條形統(tǒng)計圖;(標(biāo)上數(shù)據(jù))
③家庭過期藥品的正確處理方式是送回收站,若該市有![]() 萬戶家庭,請估計大約有多少戶家庭處理過期藥品的方式是送回收站.
萬戶家庭,請估計大約有多少戶家庭處理過期藥品的方式是送回收站.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
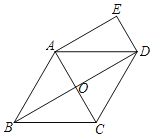
【題目】已知:如圖,在菱形ABCD中,對角線AC、BD相交于點O,DE∥AC,AE∥BD.
(1)求證:四邊形AODE是矩形;
(2)若AB=2,∠BCD=120°,求四邊形AODE的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】初中學(xué)生對待學(xué)習(xí)的態(tài)度一直是教育工作者極為關(guān)注的一個問題.為此某市教育局對本市部分學(xué)校的八年級學(xué)生對待學(xué)習(xí)的態(tài)度進(jìn)行了一次抽樣調(diào)查(把學(xué)習(xí)態(tài)度分為三個層級,A級:喜歡;B級:不太喜歡;C級:不喜歡),并將調(diào)查結(jié)果繪制成不完整的統(tǒng)計圖(如圖![]() ).請根據(jù)圖中提供的信息,解答下列問題:
).請根據(jù)圖中提供的信息,解答下列問題:
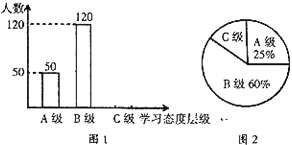
(1)此次抽樣調(diào)查中,共調(diào)查了_____名學(xué)生;
(2)將條形統(tǒng)計圖補(bǔ)充完整;
(3)求出扇形統(tǒng)計圖中![]() 級所占的圓心角的度數(shù);
級所占的圓心角的度數(shù);
(4)根據(jù)抽樣調(diào)查結(jié)果,請你估計該市近![]() 名初中生中大約有多少名學(xué)生學(xué)習(xí)態(tài)度達(dá)標(biāo).(達(dá)標(biāo)包括
名初中生中大約有多少名學(xué)生學(xué)習(xí)態(tài)度達(dá)標(biāo).(達(dá)標(biāo)包括![]() 級和
級和![]() 級)
級)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖, ![]() 是直線
是直線![]() 上的兩點,直線l1、l2的初始位置與直線
上的兩點,直線l1、l2的初始位置與直線![]() 重合將l1繞點
重合將l1繞點![]() 順時針以每秒10°的速度旋轉(zhuǎn),將l2繞點B逆時針以每秒5°的速度旋轉(zhuǎn),且兩條直線從重合位置同時開始旋轉(zhuǎn),設(shè)旋轉(zhuǎn)時間為
順時針以每秒10°的速度旋轉(zhuǎn),將l2繞點B逆時針以每秒5°的速度旋轉(zhuǎn),且兩條直線從重合位置同時開始旋轉(zhuǎn),設(shè)旋轉(zhuǎn)時間為![]() 秒(
秒(![]() 是正整數(shù)).當(dāng)
是正整數(shù)).當(dāng)![]() 時,設(shè)
時,設(shè)![]() 的交點為
的交點為![]() ;當(dāng)
;當(dāng)![]() 時,設(shè)
時,設(shè)![]() 的交點為
的交點為![]() ;當(dāng)
;當(dāng)![]() 時設(shè)
時設(shè)![]() 的交點為
的交點為![]() ……那么當(dāng)
……那么當(dāng)![]() 時,
時, ![]() 相交所得的鈍角是__________.當(dāng)
相交所得的鈍角是__________.當(dāng)![]() 落在
落在![]() 上方時,
上方時, ![]() 的最小值是__________.
的最小值是__________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
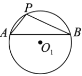
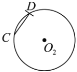
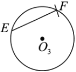
【題目】已知![]() ,
,![]() ,
,![]() 是等圓,
是等圓,![]() 內(nèi)接于
內(nèi)接于![]() ,點
,點![]() ,
,![]() 分別在
分別在![]() ,
,![]() 上.如圖,
上.如圖,
①以![]() 為圓心,
為圓心,![]() 長為半徑作弧交
長為半徑作弧交![]() 于點
于點![]() ,連接
,連接![]() ;
;
②以![]() 為圓心,
為圓心,![]() 長為半徑作弧交
長為半徑作弧交![]() 于點
于點![]() ,連接
,連接![]() ;
;
下面有四個結(jié)論:
①![]()
②![]()
③![]()
④![]()
所有正確結(jié)論的序號是( ).
A.①②③④B.①②③C.②④D.②③④
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com