
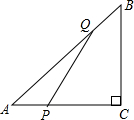
 (2008•徐匯區一模)如圖,在Rt△ABC中,∠C=90°,AB=10,sinA=
(2008•徐匯區一模)如圖,在Rt△ABC中,∠C=90°,AB=10,sinA=| 4 | 5 |
| 3 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 10 |
| RN |
| QN |
| QM |
| PM |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 8 |
| 5 |
| 18 |
| 5 |
| 9 |
| 5 |
49+
| ||
| 12 |
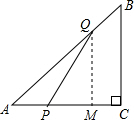 解:(1)過點Q作QM⊥AC于M,
解:(1)過點Q作QM⊥AC于M,| QM |
| AQ |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 10 |
| BC |
| AC |
| 3 |
| 5 |
| AB2-BC2 |
| 102-62 |
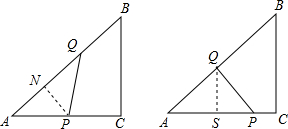 (2)分三種情況:①當AP=AQ時,有x=10-x,
(2)分三種情況:①當AP=AQ時,有x=10-x,| 3 |
| 5 |
| 4 |
| 5 |
| 1 |
| 2 |
| 10-x |
| 2 |
| 10-x |
| 2 |
| 4 |
| 5 |
| 50 |
| 13 |
| x |
| 2 |
| 4 |
| 5 |
| 80 |
| 13 |
| 50 |
| 13 |
| 80 |
| 13 |
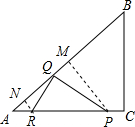 (3)存在這樣的x,使得∠PQR=90°,
(3)存在這樣的x,使得∠PQR=90°,| RN |
| QN |
| QM |
| PM |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 8 |
| 5 |
| 18 |
| 5 |
| 9 |
| 5 |
| ||||
|
10-
| ||
|
49±
| ||
| 12 |
49+
| ||
| 12 |
| 4 |
| 5 |
23-
| ||
| 15 |
| 9 |
| 5 |
53-3
| ||
| 20 |
| 8 |
| 5 |
| 18 |
| 5 |
44+2
| ||
| 15 |
| 3 |
| 5 |
49+
| ||
| 20 |
| RN |
| QM |
31+
| ||
| 30 |
| QN |
| PM |
31+
| ||
| 30 |
| RN |
| QM |
| QN |
| PM |
49-
| ||
| 12 |
49±
| ||
| 12 |


 舉一反三期末百分沖刺卷系列答案
舉一反三期末百分沖刺卷系列答案科目:初中數學 來源: 題型:
 (2008•徐匯區一模)如圖,直線l1∥l2∥l3,另兩條直線分別交l1,l2,l3于點A,B,C及點D,E,F,且AB=3,DE=4,EF=2,則BC=
(2008•徐匯區一模)如圖,直線l1∥l2∥l3,另兩條直線分別交l1,l2,l3于點A,B,C及點D,E,F,且AB=3,DE=4,EF=2,則BC=| 3 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com