
【題目】如圖,兩個同心圓,大圓半徑為5cm,小圓的半徑為4cm,若大圓的弦AB與小圓有兩個公共點,則AB的取值范圍是( )
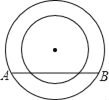
A. 4<AB<5 B. 6<AB<10 C. 6≤AB<10 D. 6<AB≤10
 全能練考卷系列答案
全能練考卷系列答案 一課一練課時達標系列答案
一課一練課時達標系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知![]()
![]() ,請用無刻度直尺和圓規,完成下列作圖(不要求寫作法,保留作圖痕跡):
,請用無刻度直尺和圓規,完成下列作圖(不要求寫作法,保留作圖痕跡):
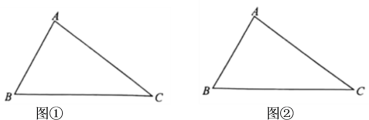
(1)在邊![]() 上找一點
上找一點![]() ,使得:將
,使得:將![]() 沿著過點
沿著過點![]() 的某一條直線折疊,點
的某一條直線折疊,點![]() 與點
與點![]() 能重合,請在圖①中作出點
能重合,請在圖①中作出點![]() ;
;
(2)在邊![]() 上找一點
上找一點![]() ,使得:將
,使得:將![]() 沿著過點
沿著過點![]() 的某一條直線折疊,點
的某一條直線折疊,點![]() 能落在邊
能落在邊![]() 上的點
上的點![]() 處,且
處,且![]() ,請在圖②中作出點
,請在圖②中作出點![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 是邊長為6的等邊三角形,
是邊長為6的等邊三角形,![]() 是
是![]() 邊上一動點,由
邊上一動點,由![]() 向
向![]() 運動(與
運動(與![]() 、
、![]() 不重合),
不重合),![]() 是
是![]() 延長線上一動點,與點
延長線上一動點,與點![]() 同時以相同的速度由
同時以相同的速度由![]() 向
向![]() 延長線方向運動(
延長線方向運動(![]() 不與
不與![]() 重合),過
重合),過![]() 作
作![]() 于
于![]() ,連接
,連接![]() 交
交![]() 于
于![]() .
.
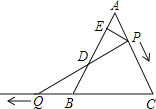
(1)當![]() 時,求
時,求![]() 的長;
的長;
(2)在運動過程中線段![]() 的長是否發生變化?如果不變,求出線段
的長是否發生變化?如果不變,求出線段![]() 的長;如果發生改變,請說明理由.
的長;如果發生改變,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
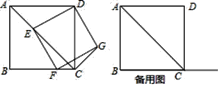
【題目】四邊形![]() 為正方形,點
為正方形,點![]() 為線段
為線段![]() 上一點,連接
上一點,連接![]() ,過點
,過點![]() 作
作![]() ,交射線
,交射線![]() 于點
于點![]() ,以
,以![]() 、
、![]() 為鄰邊作矩形
為鄰邊作矩形![]() ,連接
,連接![]() .
.
![]() 如圖
如圖![]() ,求證:矩形
,求證:矩形![]() 是正方形;
是正方形;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的長度;
的長度;
![]() 當線段
當線段![]() 與正方形
與正方形![]() 的某條邊的夾角是
的某條邊的夾角是![]() 時,直接寫出
時,直接寫出![]() 的度數.
的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
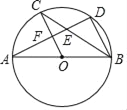
【題目】如圖,AB是⊙O的直徑,C、D是⊙O上的點,且OC∥BD,AD分別與BC、OC相較于點E、F,則下列結論:①AD⊥BD;②∠AOC=∠AEC; ③BC平分∠ABD;④△CEF≌△BED.其中一定成立的是_____(把你認為正確結論的序號都填上).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《九章算術》提供了許多整勾股數,如![]() ,
,![]() ,
,![]() ,
,![]() 等等,并把一組勾股數中最大的數稱為“弦數”.后人在此基礎上進一步研究,得到如下規律:若
等等,并把一組勾股數中最大的數稱為“弦數”.后人在此基礎上進一步研究,得到如下規律:若![]() 是大于1的奇數,把它平方后拆成相鄰的兩個整數,那么
是大于1的奇數,把它平方后拆成相鄰的兩個整數,那么![]() 與這兩個整數構成一組勾股數;若
與這兩個整數構成一組勾股數;若![]() 是大于2的偶數,把它除以2后再平方,然后把這個平方數分別減1,加l得到兩個整數,那么
是大于2的偶數,把它除以2后再平方,然后把這個平方數分別減1,加l得到兩個整數,那么![]() 與這兩個整數構成一組勾股數.由上述方法得到的勾股數稱為“由
與這兩個整數構成一組勾股數.由上述方法得到的勾股數稱為“由![]() 生成的勾股數”.若“由9生成的勾股數”的“弦數“記為
生成的勾股數”.若“由9生成的勾股數”的“弦數“記為![]() ,“由20生成的勾股數”的“弦數“記為
,“由20生成的勾股數”的“弦數“記為![]() ,則
,則![]() __________.
__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
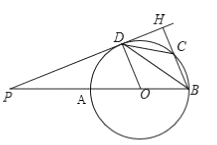
【題目】如圖,在⊙O中,點P為直徑BA延長線上一點,PD切⊙O于點D、過點B作BH⊥PH,點H為垂足,BH交⊙O于點C,連接BD,CD.
(1)求證:BD平分∠ABH;
(2)若CD=2,∠ABD=30°,求⊙O的直徑的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com