
【題目】如圖,![]() 中,
中,![]() ,
,![]() ,
,![]() ,若動點
,若動點![]() 從點
從點![]() 開始,按
開始,按![]() 的路徑運動,且速度為每秒
的路徑運動,且速度為每秒![]() ,設出發的時間為
,設出發的時間為![]() 秒.
秒.

(1)出發2秒后,求![]() 的周長.
的周長.
(2)問![]() 為何值時,
為何值時,![]() 為等腰三角形?
為等腰三角形?
(3)另有一點![]() ,從點
,從點![]() 開始,按
開始,按![]() 的路徑運動,且速度為每秒
的路徑運動,且速度為每秒![]() ,若
,若![]() 、
、![]() 兩點同時出發,當
兩點同時出發,當![]() 、
、![]() 中有一點到達終點時,另一點也停止運動.當
中有一點到達終點時,另一點也停止運動.當![]() 為何值時,直線
為何值時,直線![]() 把
把![]() 的周長分成
的周長分成![]() 的兩部分?
的兩部分?
【答案】(1)![]() cm;(2)當
cm;(2)當![]() 為3秒、5.4秒、6秒、6.5秒時,
為3秒、5.4秒、6秒、6.5秒時,![]() 為等腰三角形;(3)
為等腰三角形;(3)![]() 或
或![]() 或
或![]() 秒
秒
【解析】
(1)根據速度為每秒1cm,求出出發2秒后CP的長,然后就知AP的長,利用勾股定理求得PB的長,最后即可求得周長;
(2)分點P在邊AC上和點P在邊AB上兩種情況求解即可;
(3)分類討論:①當![]() 點在
點在![]() 上,
上,![]() 在
在![]() 上;②當
上;②當![]() 點在
點在![]() 上,
上,![]() 在
在![]() 上;③當
上;③當![]() 點在
點在![]() 上,
上,![]() 在
在![]() 上.
上.
解:(1)如圖1,由![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
動點![]() 從點
從點![]() 開始,按
開始,按![]() 的路徑運動,且速度為每秒
的路徑運動,且速度為每秒![]() ,
,
∴出發2秒后,則![]() ,
,
∴AP=2,
∵![]() ,
,
∴![]() ,
,
∴![]() 的周長為:
的周長為:![]() .
.
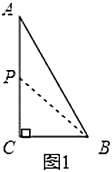
(2)①如圖2,若![]() 在邊
在邊![]() 上時,
上時,![]() ,
,
此時用的時間為![]() ,
,![]() 為等腰三角形;
為等腰三角形;
②2若![]() 在
在![]() 邊上時,有三種情況:
邊上時,有三種情況:
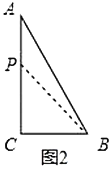
(ⅰ)如圖3,若使![]() ,此時
,此時![]() ,
,![]() 運動的路程為
運動的路程為![]() ,
,
所以用的時間為![]() ,
,![]() 為等腰三角形;
為等腰三角形;
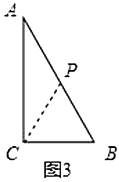
(ⅱ)如圖4,若![]() ,作
,作![]() 于點
于點![]() ,
,
∵![]() ,
,
∴CD=![]() ,
,
在![]() 中,
中,
![]() ,
,
所以![]() ,
,
所以![]() 運動的路程為
運動的路程為![]() ,
,
則用的時間為![]() ,
,![]() 為等腰三角形;
為等腰三角形;
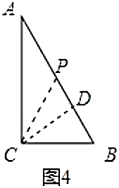
(ⅲ)如圖5,若![]() ,此時
,此時![]() 應該為斜邊
應該為斜邊![]() 的中點,
的中點,![]() 運動的路程為
運動的路程為![]() ,
,
則所用的時間為![]() ,
,![]() 為等腰三角形;
為等腰三角形;
綜上所述,當![]() 為
為![]() 、
、![]() 、
、![]() 、
、![]() 時,
時,![]() 為等腰三角形;
為等腰三角形;
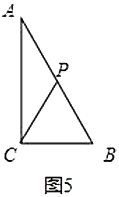
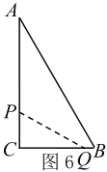
(3)①3÷2=1.5秒,如圖6,當![]() 點在
點在![]() 上,
上,![]() 在
在![]() 上,則
上,則![]() ,
,![]() ,
,
∵直線![]() 把
把![]() 的周長分成
的周長分成![]() 的兩部分,
的兩部分,
∴![]() ,∴
,∴![]() ,符合題意;
,符合題意;
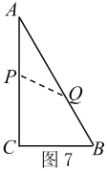
②(3+5) ÷2=4秒,如圖7,當![]() 點在
點在![]() 上,
上,![]() 在
在![]() 上,則
上,則![]() ,
,![]() ,
,
∵直線![]() 把
把![]() 的周長分成
的周長分成![]() 的兩部分,
的兩部分,
∴![]() ,
,![]() ,符合題意;
,符合題意;
③12÷2=6秒,當![]() 點在
點在![]() 上,
上,![]() 在
在![]() 上,則
上,則![]() ,
,![]() ,
,
∵直線![]() 把
把![]() 的周長分成
的周長分成![]() 的兩部分,
的兩部分,
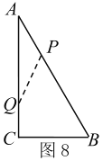
(ⅰ)當AP+AQ=周長的![]() 時,如圖8,
時,如圖8,
∴![]() ,
,![]() ,符合題意;
,符合題意;
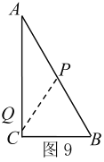
(ⅱ)當AP+AQ=周長的![]() 時,如圖9,
時,如圖9,
∴![]() ,∴
,∴![]() ;
;
∵當![]() 秒時,點
秒時,點![]() 到達
到達![]() 點停止運動,
點停止運動,
∴![]() 這種情況應該舍去.
這種情況應該舍去.
綜上,當![]() 為
為![]() 或
或![]() 或
或![]() 秒時,直線
秒時,直線![]() 把
把![]() 的周長分成
的周長分成![]() 的兩部分.
的兩部分.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC 中,D,E 分別是 AB,BC 上的點,且 DE∥AC,若 S△BDE:S△CDE=1:3,則S△DEB: S△ADC=( )

A. 1:5 B. 1:9 C. 1:10 D. 1:12
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某高中學校為使高一新生入校后及時穿上合身的校服,現提前對某校九年級三班學生即將所穿校服型號情況進行了摸底調查,并根據調查結果繪制了如下兩個不完整的統計圖(校服型號以身高作為標準,共分為6種型號).
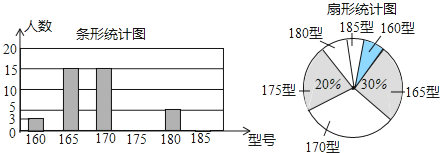
根據以上信息,解答下列問題:
(Ⅰ)該班共有 名學生,其中穿175型校服的學生有 名;
(Ⅱ)在條形統計圖中,請把空缺部分補充完整.
(Ⅲ)在扇形統計圖中,185型校服所對應的扇形圓心角的大小為 ;
(Ⅳ)該班學生所穿校服型號的眾數為 ,中位數為 .
(Ⅴ)如果該校預計招收新生600名,根據樣本數據,估計新生中穿170型校服的學生大約有 名.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC的面積為8cm2 , AP垂直∠B的平分線BP于P,則△PBC的面積為( )
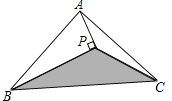
A. 2cm2 B. 3cm2 C. 4cm2 D. 5cm2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】每年的![]() 月
月![]() 日為世界環保日,為了提倡低碳環保,某公司決定購買
日為世界環保日,為了提倡低碳環保,某公司決定購買![]() 臺節省能源的新設備,現有甲、乙兩種型號的設備可供選購.經調查:購買
臺節省能源的新設備,現有甲、乙兩種型號的設備可供選購.經調查:購買![]() 臺甲型設備比購買
臺甲型設備比購買![]() 臺乙型設備多花
臺乙型設備多花![]() 萬元,購買
萬元,購買![]() 臺甲型設備比購買
臺甲型設備比購買![]() 臺乙型設備少花
臺乙型設備少花![]() 萬元.
萬元.
(1)求甲、乙兩種型號設備每臺的價格;
(2)該公司經決定購買甲型設備不少于![]() 臺,預算購買節省能源的新設備資金不超過
臺,預算購買節省能源的新設備資金不超過![]() 萬元,你認為該公司有哪幾種購買方案;
萬元,你認為該公司有哪幾種購買方案;
(3)在(2)的條件下,已知甲型設備每月的產量為![]() 噸,乙型設備每月的產量為
噸,乙型設備每月的產量為![]() 噸.若每月要求產量不低于
噸.若每月要求產量不低于![]() 噸,為了節約資金,請你為該公司設計一種最省錢的購買方案.
噸,為了節約資金,請你為該公司設計一種最省錢的購買方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
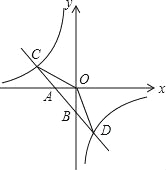
【題目】如圖,已知一次函數y1=k1x+b的圖象與x軸、y軸分別交于A、B兩點,與反比例函數![]() 的圖象分別交于C、D兩點,點D(2,﹣3),點B是線段AD的中點.
的圖象分別交于C、D兩點,點D(2,﹣3),點B是線段AD的中點.
(1)求一次函數y1=k1x+b與反比例函數![]() 的解析式;
的解析式;
(2)求△COD的面積;
(3)直接寫出y1>y2時自變量x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() 經過點E(1,0)和F(5,0),并交y軸于D(0,-5);拋物線
經過點E(1,0)和F(5,0),并交y軸于D(0,-5);拋物線![]() :
:![]() (a≠0),
(a≠0),
(1)試求拋物線![]() 的函數解析式;
的函數解析式;
(2)求證: 拋物線 ![]() 與x軸一定有兩個不同的交點;
與x軸一定有兩個不同的交點;
(3)若a=1
①拋物線![]() 、
、![]() 頂點分別為 ( , )、( , ) ;當x的取值范圍是_________ 時,拋物線
頂點分別為 ( , )、( , ) ;當x的取值范圍是_________ 時,拋物線![]() 、
、![]() 上的點的縱坐標同時隨橫坐標增大而增大;
上的點的縱坐標同時隨橫坐標增大而增大;
②已知直線MN分別與x軸、![]() 、
、![]() 分別交于點P(m,0)、M、N,且MN∥y軸,當1≤m≤5時,求線段MN的最大值。
分別交于點P(m,0)、M、N,且MN∥y軸,當1≤m≤5時,求線段MN的最大值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com