
【題目】某高中學校為使高一新生入校后及時穿上合身的校服,現提前對某校九年級三班學生即將所穿校服型號情況進行了摸底調查,并根據調查結果繪制了如下兩個不完整的統計圖(校服型號以身高作為標準,共分為6種型號).
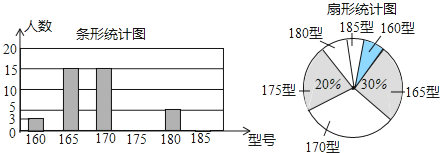
根據以上信息,解答下列問題:
(Ⅰ)該班共有 名學生,其中穿175型校服的學生有 名;
(Ⅱ)在條形統計圖中,請把空缺部分補充完整.
(Ⅲ)在扇形統計圖中,185型校服所對應的扇形圓心角的大小為 ;
(Ⅳ)該班學生所穿校服型號的眾數為 ,中位數為 .
(Ⅴ)如果該校預計招收新生600名,根據樣本數據,估計新生中穿170型校服的學生大約有 名.
【答案】(Ⅰ)50,10;(Ⅱ)補圖見解析;(Ⅲ)14.4°;(Ⅳ)165和170,170;(Ⅴ)180.
【解析】
試題(Ⅰ)根據穿165型的人數與所占的百分比列式進行計算即可求出學生總人數,再乘以175型所占的百分比計算即可得解;
(Ⅱ)先求出185型的人數,然后補全統計圖;
(Ⅲ)用185型所占的百分比乘以360°計算即可得解;
(Ⅳ)根據眾數的定義以及中位數的定義解答;
(Ⅴ)用招收新生600名乘以新生中穿170型校服的學生所占的百分比,即可求出答案.
試題解析:(Ⅰ)根據題意得:
15÷30%=50(名),
50×20%=10(名),
答:該班共有50名學生,其中穿175型校服的學生有10名;
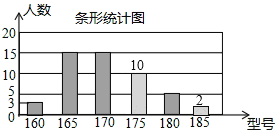
(Ⅱ)185型的學生人數為:50-3-15-15-10-5=50-48=2(名),
補全統計圖如圖所示:
(Ⅲ)185型校服所對應的扇形圓心角為:![]() ×360°=14.4°;
×360°=14.4°;
(Ⅳ)165型和170型出現的次數最多,都是15次,則眾數是165和170;
共有50個數據,第25、26個數據都是170,則中位數是170.
(Ⅴ)根據題意得:600×![]() =180(名),
=180(名),
答:新生中穿170型校服的學生大約有180名.


科目:初中數學 來源: 題型:
【題目】小明和他的同學根據拋擲兩枚硬幣時記錄的實驗結果,制作“出現兩個正面”的頻數、頻率表如下:
拋擲次數 |
|
|
|
|
|
|
|
| |
出現兩個正面的頻數 |
|
|
|
|
|
|
|
| |
出現兩個正面的頻率 |
|
|
|
|
|
|
|
|
![]() 在大數次拋擲兩枚硬幣的實驗中,出現兩個正面的頻率穩定在________附近;
在大數次拋擲兩枚硬幣的實驗中,出現兩個正面的頻率穩定在________附近;
![]() 小明和表弟玩一個拋擲兩枚硬幣的游戲,小明制定的游戲規則如下:拋出兩個正面–小明的表弟贏
小明和表弟玩一個拋擲兩枚硬幣的游戲,小明制定的游戲規則如下:拋出兩個正面–小明的表弟贏![]() 分;拋出其他結果–小明贏
分;拋出其他結果–小明贏![]() 分;誰先到
分;誰先到![]() 分,誰就得勝.你認為這個游戲規則公平嗎?說說理由.
分,誰就得勝.你認為這個游戲規則公平嗎?說說理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c的圖象與x軸交于點(﹣2,0)、(x1,0),且1<x1<2,與y軸正半軸的交點在(0,2)的下方,在原點的上方.下列結論:①4a﹣2b+c=0;②2a﹣b<0;③2a﹣b>﹣1;④2a+c<0;⑤b>a;其中正確結論的個數是( )
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,已知△ABC中,AB=10cm,AC=8cm,BC=6cm.如果點P由B出發沿BA方向點A勻速運動,同時點Q由A出發沿AC方向向點C勻速運動,它們的速度均為2cm/s.連接PQ,設運動的時間為t(單位:s)(0≤t≤4).解答下列問題:
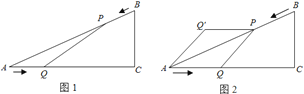
(1)當t為何值時,PQ∥BC.
(2)設△AQP面積為S(單位:cm2),當t為何值時,S取得最大值,并求出最大值.
(3)是否存在某時刻t,使線段PQ恰好把△ABC的面積平分?若存在,求出此時t的值;若不存在,請說明理由.
(4)如圖2,把△AQP沿AP翻折,得到四邊形AQPQ′.那么是否存在某時刻t,使四邊形AQPQ′為菱形?若存在,求出此時菱形的面積;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是由邊長為1的小正方形組成的![]() 網格,直線
網格,直線![]() 是一條網格線,點
是一條網格線,點![]() ,
,![]() 在格點上,
在格點上,![]() 的三個頂點都在格點(網格線的交點)上.
的三個頂點都在格點(網格線的交點)上.

(1)作出![]() 關于直線
關于直線![]() 對稱的
對稱的![]() ;
;
(2)在直線![]() 上畫出點
上畫出點![]() ,使四邊形
,使四邊形![]() 的周長最小;
的周長最小;
(3)在這個![]() 網格中,到點
網格中,到點![]() 和點
和點![]() 的距離相等的格點有_________個.
的距離相等的格點有_________個.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學為了解學生對新聞、體育、娛樂、動畫四類電視節目的喜愛情況,進行了統計調查![]() 隨機調查了某班所有同學最喜歡的節目
隨機調查了某班所有同學最喜歡的節目![]() 每名學生必選且只能選擇四類節目中的一類
每名學生必選且只能選擇四類節目中的一類![]() 并將調查結果繪成如下不完整的統計圖
并將調查結果繪成如下不完整的統計圖![]() 根據兩圖提供的信息,回答下列問題:
根據兩圖提供的信息,回答下列問題:
![]() 最喜歡娛樂類節目的有______人,圖中
最喜歡娛樂類節目的有______人,圖中![]() ______;
______;
![]() 請補全條形統計圖;
請補全條形統計圖;
![]() 根據抽樣調查結果,若該校有1800名學生,請你估計該校有多少名學生最喜歡娛樂類節目;
根據抽樣調查結果,若該校有1800名學生,請你估計該校有多少名學生最喜歡娛樂類節目;
![]() 在全班同學中,有甲、乙、丙、丁等同學最喜歡體育類節目,班主任打算從甲、乙、丙、丁4名同學中選取2人參加學校組織的體育知識競賽,請用列表法或樹狀圖求同時選中甲、乙兩同學的概率.
在全班同學中,有甲、乙、丙、丁等同學最喜歡體育類節目,班主任打算從甲、乙、丙、丁4名同學中選取2人參加學校組織的體育知識競賽,請用列表法或樹狀圖求同時選中甲、乙兩同學的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知某服裝廠現有![]() 種布料70米,
種布料70米,![]() 種布料52米,現計劃用這兩種布料生產
種布料52米,現計劃用這兩種布料生產![]() 、
、![]() 兩種型號的時裝共80套.已知做一套
兩種型號的時裝共80套.已知做一套![]() 型號的時裝需用A種布料1.1米,
型號的時裝需用A種布料1.1米,![]() 種布料0.4米,可獲利50元;做一套
種布料0.4米,可獲利50元;做一套![]() 型號的時裝需用
型號的時裝需用![]() 種布料0.6米,
種布料0.6米,![]() 種布料0.9米,可獲利45元.設生產
種布料0.9米,可獲利45元.設生產![]() 型號的時裝套數為
型號的時裝套數為![]() ,用這批布料生產兩種型號的時裝所獲得的總利潤為
,用這批布料生產兩種型號的時裝所獲得的總利潤為![]() 元.
元.
(1)求![]() (元)與
(元)與![]() (套)的函數關系式.
(套)的函數關系式.
(2)有幾種生產方案?
(3)如何生產使該廠所獲利潤最大?最大利潤是多?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 中,
中,![]() ,
,![]() ,
,![]() ,若動點
,若動點![]() 從點
從點![]() 開始,按
開始,按![]() 的路徑運動,且速度為每秒
的路徑運動,且速度為每秒![]() ,設出發的時間為
,設出發的時間為![]() 秒.
秒.

(1)出發2秒后,求![]() 的周長.
的周長.
(2)問![]() 為何值時,
為何值時,![]() 為等腰三角形?
為等腰三角形?
(3)另有一點![]() ,從點
,從點![]() 開始,按
開始,按![]() 的路徑運動,且速度為每秒
的路徑運動,且速度為每秒![]() ,若
,若![]() 、
、![]() 兩點同時出發,當
兩點同時出發,當![]() 、
、![]() 中有一點到達終點時,另一點也停止運動.當
中有一點到達終點時,另一點也停止運動.當![]() 為何值時,直線
為何值時,直線![]() 把
把![]() 的周長分成
的周長分成![]() 的兩部分?
的兩部分?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一列動車從A地開往B地,一列普通列車從B地開往A地,兩車均勻速行駛并同時出發,設普通列車行駛的時間為x(小時),兩車之間的距離為y(千米),如圖中的折線表示y與x之間的函數關系,下列說法中正確的是:( )
①AB兩地相距1000千米;②兩車出發后3小時相遇;③普通列車的速度是100千米/小時;④動車從A地到達B地的時間是4小時.
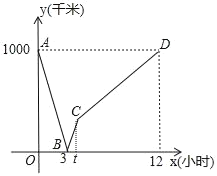
A.1個B.2個C.3個D.4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com