
【題目】問(wèn)題提出
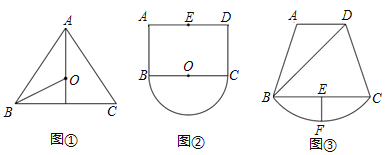
(1)如圖①,在△ABC中,AB=AC=10,BC=12,點(diǎn)O是△ABC的外接圓的圓心,則OB的長(zhǎng)為
問(wèn)題探究
(2)如圖②,已知矩形ABCD,AB=4,AD=6,點(diǎn)E為AD的中點(diǎn),以BC為直徑作半圓O,點(diǎn)P為半圓O上一動(dòng)點(diǎn),求E、P之間的最大距離;
問(wèn)題解決
(3)某地有一塊如圖③所示的果園,果園是由四邊形ABCD和弦CB與其所對(duì)的劣弧場(chǎng)地組成的,果園主人現(xiàn)要從入口D到![]() 上的一點(diǎn)P修建一條筆直的小路DP.已知AD∥BC,∠ADB=45°,BD=120
上的一點(diǎn)P修建一條筆直的小路DP.已知AD∥BC,∠ADB=45°,BD=120![]() 米,BC=160米,過(guò)弦BC的中點(diǎn)E作EF⊥BC交
米,BC=160米,過(guò)弦BC的中點(diǎn)E作EF⊥BC交![]() 于點(diǎn)F,又測(cè)得EF=40米.修建小路平均每米需要40元(小路寬度不計(jì)),不考慮其他因素,請(qǐng)你根據(jù)以上信息,幫助果園主人計(jì)算修建這條小路最多要花費(fèi)多少元?
于點(diǎn)F,又測(cè)得EF=40米.修建小路平均每米需要40元(小路寬度不計(jì)),不考慮其他因素,請(qǐng)你根據(jù)以上信息,幫助果園主人計(jì)算修建這條小路最多要花費(fèi)多少元?
【答案】(1)![]() ;(2)E、P之間的最大距離為7;(3)修建這條小路最多要花費(fèi)
;(2)E、P之間的最大距離為7;(3)修建這條小路最多要花費(fèi)![]() 元.
元.
【解析】
(1)若AO交BC于K,則AK=8,在Rt△BOK中,設(shè)OB=x,可得x2=62+(8﹣x)2,解方程可得OB的長(zhǎng);
(2)延長(zhǎng)EO交半圓于點(diǎn)P,可求出此時(shí)E、P之間的最大距離為OE+OP的長(zhǎng)即可;
(3)先求出![]() 所在圓的半徑,過(guò)點(diǎn)D作DG⊥BC,垂足為G,連接DO并延長(zhǎng)交
所在圓的半徑,過(guò)點(diǎn)D作DG⊥BC,垂足為G,連接DO并延長(zhǎng)交![]() 于點(diǎn)P,則DP為入口D到
于點(diǎn)P,則DP為入口D到![]() 上一點(diǎn)P的最大距離,求出DP長(zhǎng)即可求出修建這條小路花費(fèi)的最多費(fèi)用.
上一點(diǎn)P的最大距離,求出DP長(zhǎng)即可求出修建這條小路花費(fèi)的最多費(fèi)用.
(1)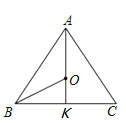
如圖,若AO交BC于K,
∵點(diǎn)O是△ABC的外接圓的圓心,AB=AC,
∴AK⊥BC,BK=![]() ,
,
∴AK=![]() ,
,
在Rt△BOK中,OB2=BK2+OK2,設(shè)OB=x,
∴x2=62+(8x)2,
解得x=![]() ,
,
∴OB=![]() ;
;
故答案為:![]() .
.
(2)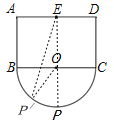
如圖,連接EO,延長(zhǎng)EO交半圓于點(diǎn)P,可求出此時(shí)E、P之間的距離最大,
∵在![]() 是任意取一點(diǎn)異于點(diǎn)P的P′,連接OP′,P′E,
是任意取一點(diǎn)異于點(diǎn)P的P′,連接OP′,P′E,
∴EP=EO+OP=EO+OP′>EP′,即EP>EP′,
∵AB=4,AD=6,
∴EO=4,OP=OC=![]() ,
,
∴EP=OE+OP=7,
∴E、P之間的最大距離為7.
(3)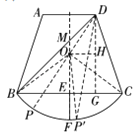
作射線(xiàn)FE交BD于點(diǎn)M,
∵BE=C,EF⊥BC,![]() 是劣弧,
是劣弧,
∴![]() 所在圓的圓心在射線(xiàn)FE上,
所在圓的圓心在射線(xiàn)FE上,
假設(shè)圓心為O,半徑為r,連接OC,則OC=r,OE=r40,BE=CE=![]() ,
,
在Rt△OEC中,r2=802+(r40)2,
解得:r=100,
∴OE=OFEF=60,
過(guò)點(diǎn)D作DG⊥BC,垂足為G,
∵AD∥BC,∠ADB=45°,
∴∠DBC=45°,
在Rt△BDG中,DG=BG=![]() ,
,
在Rt△BEM中,ME=BE=80,
∴ME>OE,
∴點(diǎn)O在△BDC內(nèi)部,
∴連接DO并延長(zhǎng)交![]() 于點(diǎn)P,則DP為入口D到
于點(diǎn)P,則DP為入口D到![]() 上一點(diǎn)P的最大距離,
上一點(diǎn)P的最大距離,
∵在![]() 上任取一點(diǎn)異于點(diǎn)P的點(diǎn)P′,連接OP′,P′D,
上任取一點(diǎn)異于點(diǎn)P的點(diǎn)P′,連接OP′,P′D,
∴DP=OD+OP=OD+OP′>DP′,即DP>DP′,
過(guò)點(diǎn)O作OH⊥DG,垂足為H,則OH=EG=40,DH=DGHG=DGOE=60,
∴![]() ,
,
∴DP=OD+r=![]() ,
,
∴修建這條小路最多要花費(fèi)40×![]() 元.
元.


 閱讀快車(chē)系列答案
閱讀快車(chē)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
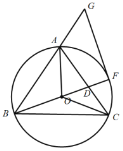
【題目】如圖,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的外接圓,連結(jié)OA、OB、OC,延長(zhǎng)BO與AC交于點(diǎn)D,與
的外接圓,連結(jié)OA、OB、OC,延長(zhǎng)BO與AC交于點(diǎn)D,與![]() 交于點(diǎn)F,延長(zhǎng)BA到點(diǎn)G,使得
交于點(diǎn)F,延長(zhǎng)BA到點(diǎn)G,使得![]() ,連接FG.
,連接FG.

備用圖
(1)求證:FG是![]() 的切線(xiàn);
的切線(xiàn);
(2)若![]() 的半徑為4.
的半徑為4.
①當(dāng)![]() ,求AD的長(zhǎng)度;
,求AD的長(zhǎng)度;
②當(dāng)![]() 是直角三角形時(shí),求
是直角三角形時(shí),求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
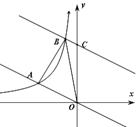
【題目】如圖,在平面直角坐標(biāo)系中,直線(xiàn)![]() 與反比例函數(shù)
與反比例函數(shù)![]()
![]() 在第二象限內(nèi)的圖象相交于點(diǎn)
在第二象限內(nèi)的圖象相交于點(diǎn)![]() ,將直線(xiàn)
,將直線(xiàn)![]() 向上平移后與反比例函數(shù)圖象在第二象限內(nèi)交于點(diǎn)
向上平移后與反比例函數(shù)圖象在第二象限內(nèi)交于點(diǎn)![]() ,與
,與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,且
,且![]() 的面積為3,則直線(xiàn)
的面積為3,則直線(xiàn)![]() 的關(guān)系式為:________
的關(guān)系式為:________
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,正方形![]() 的邊長(zhǎng)為
的邊長(zhǎng)為![]() ,
,![]() 在正方形外,
在正方形外,![]() ,過(guò)
,過(guò)![]() 作
作![]() 于
于![]() ,直線(xiàn)
,直線(xiàn)![]() ,
,![]() 交于點(diǎn)
交于點(diǎn)![]() ,直線(xiàn)
,直線(xiàn)![]() 交直線(xiàn)
交直線(xiàn)![]() 于點(diǎn)
于點(diǎn)![]() ,則下列結(jié)論正確的是( )
,則下列結(jié)論正確的是( )

①![]() ;②
;②![]() ;③
;③![]() ;
;
④若![]() ,則
,則![]()
A.1個(gè)B.2個(gè)C.3個(gè)D.4個(gè)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,菱形![]() 的邊長(zhǎng)為
的邊長(zhǎng)為![]() ,點(diǎn)
,點(diǎn)![]() 在對(duì)角線(xiàn)
在對(duì)角線(xiàn)![]() 上(點(diǎn)
上(點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 的左側(cè)),且
的左側(cè)),且![]() 則
則![]() 的最小值為____.
的最小值為____.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
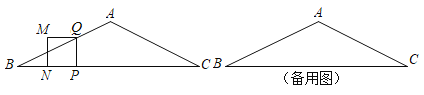
【題目】如圖,在![]() 中,
中,![]() ,
,![]() .動(dòng)點(diǎn)
.動(dòng)點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā),沿
出發(fā),沿![]() 以每秒
以每秒![]() 個(gè)單位長(zhǎng)度的速度向終點(diǎn)
個(gè)單位長(zhǎng)度的速度向終點(diǎn)![]() 運(yùn)動(dòng),當(dāng)點(diǎn)
運(yùn)動(dòng),當(dāng)點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 、
、![]() 不重合時(shí),過(guò)點(diǎn)
不重合時(shí),過(guò)點(diǎn)![]() 作
作![]() 交折線(xiàn)
交折線(xiàn)![]() 于點(diǎn)
于點(diǎn)![]() ,以
,以![]() 為邊向左作正方形
為邊向左作正方形![]() .設(shè)正方形
.設(shè)正方形![]() 與
與![]() 重疊部分圖形的面積為
重疊部分圖形的面積為![]() (平方單位),點(diǎn)
(平方單位),點(diǎn)![]() 運(yùn)動(dòng)的時(shí)間為
運(yùn)動(dòng)的時(shí)間為![]() (秒).
(秒).
備用圖
(1)用含![]() 的代數(shù)式表示
的代數(shù)式表示![]() 的長(zhǎng).
的長(zhǎng).
(2)直接寫(xiě)出點(diǎn)![]() 在
在![]() 內(nèi)部時(shí)
內(nèi)部時(shí)![]() 的取值范圍.
的取值范圍.
(3)求![]() 與
與![]() 之間的函數(shù)關(guān)系式.
之間的函數(shù)關(guān)系式.
(4)直接寫(xiě)出點(diǎn)![]() 落在
落在![]() 的中位線(xiàn)所在直線(xiàn)上時(shí)
的中位線(xiàn)所在直線(xiàn)上時(shí)![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,矩形ABCD中,E是AD的中點(diǎn),延長(zhǎng)CE,BA交于點(diǎn)F,連接AC,DF.
(1)求證:四邊形ACDF是平行四邊形;
(2)當(dāng)CF平分∠BCD時(shí),寫(xiě)出BC與CD的數(shù)量關(guān)系,并說(shuō)明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知點(diǎn)![]() ,
,![]() 在二次函數(shù)
在二次函數(shù)![]() 的圖象上,點(diǎn)
的圖象上,點(diǎn)![]() 是函數(shù)圖象的頂點(diǎn),則( )
是函數(shù)圖象的頂點(diǎn),則( )
A.當(dāng)![]() 時(shí),
時(shí),![]() 的取值范圍是
的取值范圍是![]()
B.當(dāng)![]() 時(shí),
時(shí),![]() 的取值范圍是
的取值范圍是![]()
C.當(dāng)![]() 時(shí),
時(shí),![]() 的取值范圍是
的取值范圍是![]()
D.當(dāng)![]() 時(shí),
時(shí),![]() 的取值范圍是
的取值范圍是![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】詩(shī)詞是我國(guó)古代文化中的瑰寶,某市教育主管部門(mén)為了解本市初中生對(duì)詩(shī)詞的學(xué)習(xí)情況;舉了一次“中華詩(shī)詞”背誦大賽,隨機(jī)抽取了部分同學(xué)的成絨(![]() 為整數(shù),總分100分),繪制了如下尚不完整的統(tǒng)計(jì)圖表.
為整數(shù),總分100分),繪制了如下尚不完整的統(tǒng)計(jì)圖表.
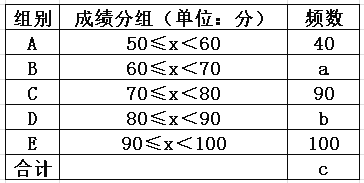

根據(jù)以上信息解答下列問(wèn)題:
(1)統(tǒng)計(jì)表中![]() ________,
________,![]() ________,
________,![]() ________;
________;
(2)扇形統(tǒng)計(jì)圖中,![]() 的值為________,“
的值為________,“![]() ”所對(duì)應(yīng)的圓心角的度數(shù)是________(度);
”所對(duì)應(yīng)的圓心角的度數(shù)是________(度);
(3)若參加本次大賽的同學(xué)共有4000人,請(qǐng)你估計(jì)成績(jī)?cè)?/span>80分及以上的學(xué)生大約有多少人?
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com