
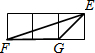
 如圖,小正方形的邊長均為1,則下面4個陰影部分三角形中,能與△EFG相似的是( )
如圖,小正方形的邊長均為1,則下面4個陰影部分三角形中,能與△EFG相似的是( )| A. | 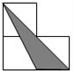 | B. |  | C. | 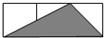 | D. | 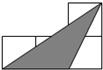 |
分析 根據相似三角形的判定,易得出△ABC的三邊的邊長,故只需分別求出各選項中三角形的邊長,分析兩三角形對應邊是否成比例即可.
解答 解:∵小正方形的邊長為1,
∴在△ABC中,EG=$\sqrt{2}$,FG=2,EF=$\sqrt{1+{3}^{2}}$=$\sqrt{10}$,
A中,一邊=1,一邊=$\sqrt{5}$,一邊=2$\sqrt{2}$,三邊與△ABC中的三邊不能對應成比例,故兩三角形不相似.故A錯誤;
B中,一邊=1,一邊=$\sqrt{2}$,一邊=$\sqrt{{2}^{2}+1}$=$\sqrt{5}$,有$\frac{\sqrt{2}}{1}$=$\frac{2}{\sqrt{2}}$=$\frac{\sqrt{10}}{\sqrt{5}}$,即三邊與△ABC中的三邊對應成比例,故兩三角形相似.故B正確;
C中,一邊=3,一邊=$\sqrt{2}$,一邊=$\sqrt{1+{2}^{2}}$=$\sqrt{5}$,三邊與△ABC中的三邊不能對應成比例,故兩三角形不相似.故C錯誤;
D中,一邊=2,一邊=$\sqrt{5}$,一邊=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,三邊與△ABC中的三邊不能對應成比例,故兩三角形不相似.故D錯誤.
故選B.
點評 本題考查了相似三角形的判定及勾股定理,識別兩三角形相似,除了要掌握定義外,還要注意正確找出兩三角形的對應邊、對應角,可利用數形結合思想根據圖形提供的數據計算對應角的度數、對應邊的比.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
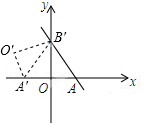 如圖,直線y=-$\sqrt{3}$x+4$\sqrt{3}$與x軸、y軸分別交于A、B兩點,把△AOB繞點B逆時針旋轉,點A在x軸上,得到△A′O′B,則點O′的坐標是( )
如圖,直線y=-$\sqrt{3}$x+4$\sqrt{3}$與x軸、y軸分別交于A、B兩點,把△AOB繞點B逆時針旋轉,點A在x軸上,得到△A′O′B,則點O′的坐標是( )| A. | (-2,2$\sqrt{3}$) | B. | (6,2$\sqrt{3}$) | C. | (2,2$\sqrt{3}$) | D. | (-6,2$\sqrt{3}$) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
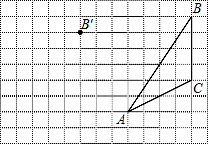 如圖,在方格紙內將三角形ABC經過平移后得到三角形A′B′C′,圖中標出了點B的對應點B′,解答下列問題.
如圖,在方格紙內將三角形ABC經過平移后得到三角形A′B′C′,圖中標出了點B的對應點B′,解答下列問題.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com