
【題目】如圖,在平面直角坐標系中,二次函數![]() 的圖像交
的圖像交![]() 軸于
軸于![]() ,
,![]() 兩點,交
兩點,交![]() 軸于點
軸于點![]() ,連接
,連接![]() ,已知
,已知![]() .
.
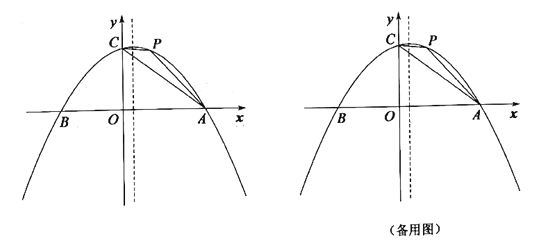
(1)點![]() 的坐標是______;
的坐標是______;
(2)若點![]() 是拋物線上的任意一點,連接
是拋物線上的任意一點,連接![]() 、
、![]() .
.
①當![]() 與
與![]() 的面積相等時,求點
的面積相等時,求點![]() 的坐標;
的坐標;
②把![]() 沿著
沿著![]() 翻折,若點
翻折,若點![]() 與拋物線對稱軸上的點
與拋物線對稱軸上的點![]() 重合,直接寫出點
重合,直接寫出點![]() 的橫坐標.
的橫坐標.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)根據![]() ,
,![]() ,即可得出答案;
,即可得出答案;
(2)將點A、C的坐標代入拋物線解析式,求出a、c的值,即可得出拋物線解析式為![]() ,線段AC所在直線的解析式為
,線段AC所在直線的解析式為![]() .利用勾股定理可求出AC=10,
.利用勾股定理可求出AC=10,![]() 的面積為
的面積為![]() ,根據面積相等,即可得出點P到AC的距離為
,根據面積相等,即可得出點P到AC的距離為![]() 設點P的坐標為
設點P的坐標為![]() ,根據點到直線的距離公式即可求出點P到AC的距離,解方程即可得出答案;
,根據點到直線的距離公式即可求出點P到AC的距離,解方程即可得出答案;
(3)根據題意可設設點P的坐標為![]() ,點Q的坐標為
,點Q的坐標為![]() ,因為
,因為![]() ,可根據直線AC、PQ斜率相乘等于-1,線段PQ的中點位于直線AC上列方程組求解.
,可根據直線AC、PQ斜率相乘等于-1,線段PQ的中點位于直線AC上列方程組求解.
解:(1)∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
故答案為:![]() ;
;
(2)將點![]() 、
、![]() 代入
代入![]() 可得出:
可得出:![]()
∴拋物線解析式為![]()
將點![]() 、
、![]() 代入直線AC的解析式
代入直線AC的解析式![]()
∴AC所在直線解析式為:![]()
∵![]()
∴![]() 的面積為
的面積為![]()
∴![]()
∴根據![]() 與
與![]() 的面積相等,得出點P到AC的距離為
的面積相等,得出點P到AC的距離為![]()
設點P的坐標為![]()
∴
整理可得:![]()
∴![]() 或
或![]()
整理得出: ![]() (無解)或
(無解)或![]()
解得:![]()
代入拋物線解析式即可求出點P的縱坐標為![]()
∴點P的坐標為![]() 或
或![]() ;
;
(3)如下圖所示,![]()
拋物線![]() 的對稱軸為
的對稱軸為![]()
設點P的坐標為![]() ,點Q的坐標為
,點Q的坐標為![]()
∴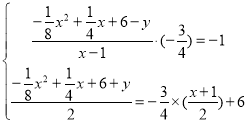
整理可得出:

可得:![]()
解得:![]()
即點P的橫坐標為:![]() .
.


科目:初中數學 來源: 題型:
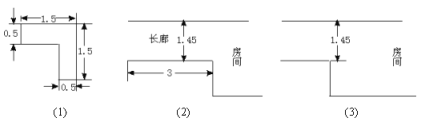
【題目】如圖(1)所示是某立式家具(角書櫥)的橫斷面,請你設計一個方案(角書櫥高2米,房間高2.6米,所以不必從高度方面考慮方案的設計),按此方案,可使該家具通過圖(2)中的長廊搬入房間.在圖(3)中把你設計的方案畫成草圖,并說明按此方案可把家具搬入房間的理由(注:搬運過程中不準拆卸家具,不準損壞墻壁).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數![]() 的圖象與
的圖象與![]() 軸的一個交點為
軸的一個交點為![]() ,另一個交點為
,另一個交點為![]() ,且與
,且與![]() 軸相交于
軸相交于![]() 點
點
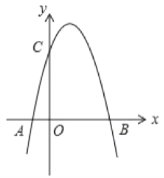
(1)則![]() _________;
_________;![]() 點坐標為___________;
點坐標為___________;
(2)在直線![]() 上方的拋物線上是否存在一點
上方的拋物線上是否存在一點![]() ,使得它與
,使得它與![]() ,
,![]() 兩點構成的三角形面積最大,若存在,求出此時
兩點構成的三角形面積最大,若存在,求出此時![]() 點坐標;若不存在,請簡要說明理由.
點坐標;若不存在,請簡要說明理由.
(3)![]() 為拋物線上一點,它關于直線
為拋物線上一點,它關于直線![]() 的對稱點為
的對稱點為![]()
①當四邊形![]() 為菱形時,求點
為菱形時,求點![]() 的坐標;
的坐標;
②點![]() 的橫坐標為
的橫坐標為![]() ,當
,當![]() ________時,四邊形
________時,四邊形![]() 的面積最大.
的面積最大.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線![]() 的對稱軸為直線
的對稱軸為直線![]() ,且拋物線與
,且拋物線與![]() 軸交于
軸交于![]() 、
、![]() 兩點,與
兩點,與![]() 軸交于
軸交于![]() 點,其中
點,其中![]() ,
,![]() .
.

(1)若直線![]() 經過
經過![]() 、
、![]() 兩點,求直線
兩點,求直線![]() 和拋物線的解析式;
和拋物線的解析式;
(2)在拋物線的對稱軸![]() 上找一點
上找一點![]() ,使點
,使點![]() 到點
到點![]() 的距離與到點
的距離與到點![]() 的距離之和最小,求出點
的距離之和最小,求出點![]() 的坐標;
的坐標;
(3)設點![]() 為拋物線的對稱軸
為拋物線的對稱軸![]() 上的一個動點,求使
上的一個動點,求使![]() 為直角三角形的點
為直角三角形的點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一次班級數學測試中,65分為及格分數線,全班的總平均分為66分,而所有成績及格的學生的平均分為72分,所有成績不及格的學生的平均分為58分,為了減少不及格的學生人數,老師給每位學生的成績加上了5分,加分之后,所有成績及格的學生的平均分變為75分,所有成績不及格的學生的平均分變為59分,已知該班學生人數大于15人少于30人,該班共有_____位學生.
查看答案和解析>>
科目:初中數學 來源: 題型:
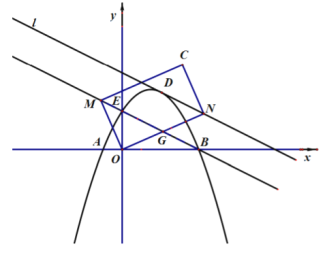
【題目】已知:如圖,二次函數![]() 的圖象交
的圖象交![]() 軸于
軸于![]() 點和
點和![]() 點(
點(![]() 點在
點在![]() 點左則),交
點左則),交![]() 軸于
軸于![]() 點,作直線
點,作直線![]() 是直線
是直線![]() 上方拋物線上的一個動點.過
上方拋物線上的一個動點.過![]() 點作 直線
點作 直線![]() 平行于直線
平行于直線![]() 是直線
是直線 ![]() 上的任意點,
上的任意點,![]() 是直線
是直線![]() 上的任意點,連接
上的任意點,連接![]() ,始終保持
,始終保持![]() 為
為![]() ,以
,以![]() 和
和![]() 邊,作矩形
邊,作矩形![]() .
.
(1)在![]() 點移動過程中,求出當
點移動過程中,求出當![]() 的面積最大時點
的面積最大時點![]() 的坐標;在
的坐標;在![]() 的面積最大 時,求矩形
的面積最大 時,求矩形![]() 的面積的最小值.
的面積的最小值.
(2)在![]() 的面積最大時,線段
的面積最大時,線段![]() 交直線
交直線![]() 于點
于點![]() ,當點
,當點![]() 四個點組成平行 四邊形時,求此時線段
四個點組成平行 四邊形時,求此時線段![]() 與拋物線的交點坐標.
與拋物線的交點坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
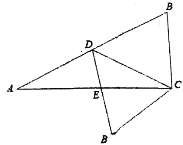
【題目】已知Rt△ABC,∠ACB=90,BC=10,AC=20,點D為斜邊中點,連接CD,將△BCD沿CD翻折得△B’CD,B’D交AC于點E,則![]() 的值為( )
的值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點E、F在四邊形ABCD的對角線延長線上,AE=CF,DE∥BF,∠1=∠2.
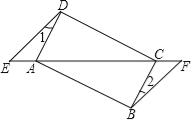
(1)求證:△AED≌△CFB;
(2)若AD⊥CD,四邊形ABCD是什么特殊四邊形?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com