
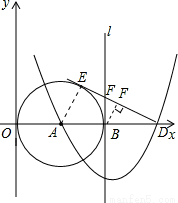
如圖,已知點A(3,0),以A為圓心作⊙A與Y軸切于原點,與x軸的另一個交點為B,過B作⊙A的切線l.
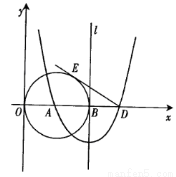
(1)以直線l為對稱軸的拋物線過點A及點C(0,9),求此拋物線的解析式;
(2)拋物線與x軸的另一個交點為D,過D作⊙A的切線DE,E為切點,求DE的長;
(3)點F是切線DE上的一個動點,當△BFD與△EAD相似時,求出BF的長 .
(1)y=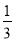 (x-6)2-3.(2)3
(x-6)2-3.(2)3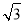 .(3)
.(3)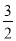 或
或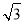 .
.
【解析】
試題分析:(1)已知了拋物線的頂點坐標,可將拋物線的解析式設為頂點坐標式,然后將C點坐標代入求解即可.
(2)由于DE是⊙A的切線,連接AE,那么根據切線的性質知AE⊥DE,在Rt△AED中,AE、AB是圓的半徑,即AE=OA=AB=3,而A、D關于拋物線的對稱軸對稱,即AB=BD=3,由此可得到AD的長,進而可利用勾股定理求得切線DE的長.
(3)若△BFD與EAD△相似,則有兩種情況需要考慮:①△AED∽△BFD,②△AED∽△FBD,根據不同的相似三角形所得不同的比例線段即可求得BF的長.
試題解析:(1)設拋物線的解析式為y=a(x-6)2+k;
∵拋物線經過點A(3,0)和C(0,9),
∴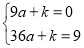 ,
,
解得:
∴y=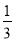 (x-6)2-3.
(x-6)2-3.
(2)連接AE;
∵DE是⊙A的切線,
∴∠AED=90°,AE=3,
∵直線l是拋物線的對稱軸,點A,D是拋物線與x軸的交點,
∴AB=BD=3,
∴AD=6;
在Rt△ADE中,DE2=AD2-AE2=62-32=27,
∴DE=3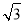 .
.
(3)當BF⊥ED時;
∵∠AED=∠BFD=90°,∠ADE=∠BDF,
∴△AED∽△BFD,
∴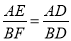 ,
,
即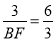 ,
,
∴BF=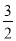 ;
;
當FB⊥AD時,
∵∠AED=∠FBD=90°,∠ADE=∠FDB,
∴△AED∽△FBD,
∴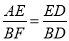 ,
,
即BF=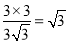 ;
;
∴BF的長為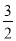 或
或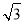 .
.
考點:二次函數綜合題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源:2014-2015學年山東省日照市莒縣北五校九年級上學期12月聯考數學試卷(解析版) 題型:解答題
(14分)如圖,⊙O的直徑AB=4,點P是AB延長線上的一點,過P點作⊙O 的切線,切點為C,連結AC.
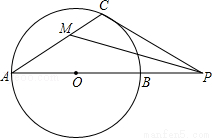
(1)若∠CPA=30°,求PC的長;
(2)若點P在AB的延長線上運動,∠CPA的平分線交AC于點M.你認為∠CMP的大小是否發生變化?若變化,請說明理由;若不變化,求出∠CMP的大小.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年遼寧省丹東市九年級上學期第二次月考數學試卷(解析版) 題型:選擇題
小軍旅行箱的密碼是一個六位數,由于他忘記了密碼的末位數字,則小軍能一次打開旅行箱的概率是( )
A、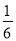 B、
B、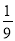 C、
C、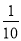 D、
D、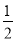
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省泰興市九年級上學期期中考試數學試卷(解析版) 題型:選擇題
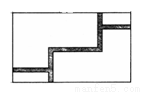
如圖,在寬為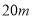 ,長為
,長為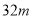 的矩形地面上修筑同樣寬的道路(圖中陰影部分),余下的部分種上草坪.要使草坪的面積為
的矩形地面上修筑同樣寬的道路(圖中陰影部分),余下的部分種上草坪.要使草坪的面積為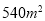 ,求道路的寬. 如果設小路寬為
,求道路的寬. 如果設小路寬為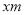 ,根據題意,所列方程正確的是( ).
,根據題意,所列方程正確的是( ).
A.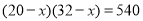 B.
B.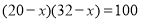
C.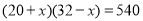 D.
D.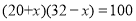
查看答案和解析>>
科目:初中數學 來源:2014-2015學年河北省沙河市九年級上學期期末模擬考試數學試卷(解析版) 題型:解答題
如圖,反比例函數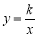 (k≠0)的圖像過等邊三角形AOB的頂點A,已知點B(-2,0)
(k≠0)的圖像過等邊三角形AOB的頂點A,已知點B(-2,0)
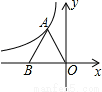
(1)求反比例函數的表達式;
(2)若要使點B在上述反比例函數的圖像上,需將△AOB向上平移多少個單位長度?
查看答案和解析>>
科目:初中數學 來源:2014-2015學年河北省沙河市九年級上學期期末模擬考試數學試卷(解析版) 題型:選擇題
如圖,Rt△ABC中,∠C=90°,AC=3,BC=4,若以A為旋轉中心,將其按順時針方向旋轉60°到△AB'C'位置,則B點經過的路線長為( )
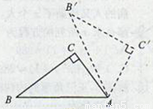
A.π B.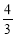 π C.
π C.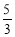 π D.
π D.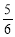 π
π
查看答案和解析>>
科目:初中數學 來源:2014-2015學年河北省沙河市九年級上學期第二次月度聯考數學試卷(解析版) 題型:解答題
如圖,⊙O1與⊙O2相交于A、B兩點,若AB=O1A=4,O2A=2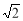 .
.
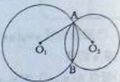
求:(1)∠O1AO2的度數;(2)O1與O2之間的距離。
查看答案和解析>>
科目:初中數學 來源:2014-2015學年河北省沙河市九年級上學期第四次月考數學試卷(解析版) 題型:選擇題
下列命題中,正確的是( )
①頂點在圓周上的角是圓周角;
②90°的圓周角所對的弦是直徑;
③圓周角度數等于圓心角度數的一半;
④三點確定一個圓;
⑤同弧所對的圓周角相等.
A.①②③ B.③④⑤ C.②⑤ D.②③
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com