
 已知二次函數(shù)y=ax2+bx+c(a≠0)的圖象如圖所示,則下列結(jié)論:
已知二次函數(shù)y=ax2+bx+c(a≠0)的圖象如圖所示,則下列結(jié)論:| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
分析 (1)根據(jù)拋物線開口向上可得出a>0,再求出拋物線的對稱軸方程可對b作出判斷;
(2)根據(jù)拋物線與x軸有兩個交點可進行判斷;
(3)拋物線的對稱軸為直線x=2可得出b=-4a,再由x=-1時y=0可得出a-b+c=0,故c=-5a,再代入
4a+b+c即可得出結(jié)論;
(4)根據(jù)拋物線的對稱性可以得出結(jié)論;
(5)根據(jù)1和3關(guān)于直線x=2對稱可得出結(jié)論.
解答 解:(1)∵拋物線開口向上,
∴a>0.
∵拋物線與x軸的交點為(-1,0),(5,0),
∴拋物線的對稱軸為直線x=-$\frac{b}{2a}$=2>0,
∴b<0,
∵a,b異號,故本小題錯誤;
(2)∵拋物線與x軸有兩個交點,
∴△=b2-4ac>0,故本小題正確;
(3)∵拋物線的對稱軸為直線x=2,
∴-$\frac{b}{2a}$=2,即b=-4a.
∵x=-1時y=0,
∴a-b+c=0,
∴c=-5a,
∴4a+b+c=4a-4a-5a=-5a<0,
∴4a+b+c<0,故本小題錯誤;
(4)∵拋物線的對稱軸為直線x=2,且拋物線與y軸的交點為(0,-2)
∴當y=2時,x=0或4,故本小題錯誤;
(5)∵當x=1和x=3距離對稱軸x=2的距離相同,
∴當x=1和x=3時,函數(shù)值相等,故本小題正確.
故選B.
點評 本題考查的是二次函數(shù)的圖象與系數(shù)的關(guān)系,解答此類問題的關(guān)鍵是掌握二次函數(shù)y=ax2+bx+c系數(shù)符號由拋物線開口方向、對稱軸、拋物線與y軸的交點、拋物線與x軸交點的個數(shù)確定,解題時要注意數(shù)形結(jié)合思想的運用.


科目:初中數(shù)學 來源:2016-2017學年四川省眉山市第九年級下學期第一次月考數(shù)學試卷(解析版) 題型:填空題
已知實數(shù)x、y滿足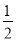 x2+2x+y-1=0,則x+2y的最大值為_________ .
x2+2x+y-1=0,則x+2y的最大值為_________ .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 網(wǎng)上購物已經(jīng)成為當今年輕人的一種潮流生活,同時也催生了快遞行業(yè)的高速發(fā)展.在剛剛過去的2016年“雙十一”活動大促銷的當天,小明欲購買一部分商品,經(jīng)了解有甲、乙兩家快遞公司分別給出了快遞費y(元)與物品重量x(千克)之間的函數(shù)圖象,根據(jù)圖象中的有關(guān)數(shù)據(jù)解答下列問題:
網(wǎng)上購物已經(jīng)成為當今年輕人的一種潮流生活,同時也催生了快遞行業(yè)的高速發(fā)展.在剛剛過去的2016年“雙十一”活動大促銷的當天,小明欲購買一部分商品,經(jīng)了解有甲、乙兩家快遞公司分別給出了快遞費y(元)與物品重量x(千克)之間的函數(shù)圖象,根據(jù)圖象中的有關(guān)數(shù)據(jù)解答下列問題:查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
 如圖,PA、PB分別切⊙O于點A、B,點E是⊙O上一點,且∠AEB=60°,則∠P=( )
如圖,PA、PB分別切⊙O于點A、B,點E是⊙O上一點,且∠AEB=60°,則∠P=( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | (a+0.8b)元 | B. | (a+1.25b)元 | C. | (b+0.8a)元 | D. | (b+1.25a)元 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | -3,-6 | B. | 3,-6 | C. | -3,-6 | D. | 3,6 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com