
【題目】已知點A(s,t)在反比例函數![]() (k為常數,k≠0)的圖象上.
(k為常數,k≠0)的圖象上.
(1)當s=﹣1,t=3時,則k= ;
(2)當點A在第二象限時,將雙曲線![]() (x<0)沿著y軸翻折,翻折后的曲線與原曲線記為曲線L,與過A點的直線y=b(b>0)交于點C,連接AO,過點O作AO的垂線與直線y=b交于點B.
(x<0)沿著y軸翻折,翻折后的曲線與原曲線記為曲線L,與過A點的直線y=b(b>0)交于點C,連接AO,過點O作AO的垂線與直線y=b交于點B.
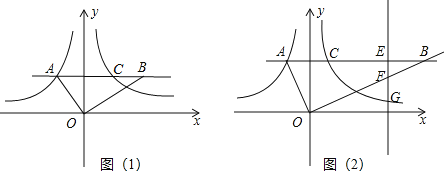
①如圖(1),當![]() 時,求
時,求![]() 值;
值;
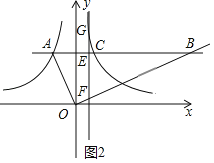
②如圖(2),若A(﹣1,![]() ),作直線x=n(n>0)交曲線L于G點,分別交射線AB,射線OB于點E,F,當
),作直線x=n(n>0)交曲線L于G點,分別交射線AB,射線OB于點E,F,當![]() 時,直接寫出n的取值范圍.
時,直接寫出n的取值范圍.
【答案】(1)-3;(2)①![]() ;②0<n<3﹣
;②0<n<3﹣![]() 或1+
或1+![]() <n<3+
<n<3+![]() .
.
【解析】
(1)將點A坐標代入解析式可求k;
(2)①設直線y=b與y軸交于點D,由題意可證△AOD∽△OBD,可得![]() ,即可求解;
,即可求解;
②分當0<n<1時,當1<n<![]() 時,當
時,當![]() <n<3時,當n>3時,四種情況討論即可.
<n<3時,當n>3時,四種情況討論即可.
解:(1)∵點A(s,t)在反比例函數![]() 的圖象上,且s=﹣1,t=3,
的圖象上,且s=﹣1,t=3,
∴k=st=﹣3
故答案為﹣3.
(2)①如圖,設直線y=b與y軸交于點D,

∵點A與點C關于y軸對稱,
∴C(﹣s,t),AD=CD=﹣s,OD=t.
∵OA⊥OB,
∴∠AOB=∠ADO=∠ODB=90°,
∴∠OAD+∠OBD=∠OAD+∠AOD=90°,
∴∠AOD=∠OBD,
∴△AOD∽△OBD,
∴![]() ,
,
∴BD=![]() ,
,
∴BC=BD﹣CD=![]() ,
,
∵![]() ,即3AC=2BC,
,即3AC=2BC,
∴3(﹣2s)=2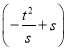 ,
,
整理得:t2=4s2,即|t|=2|s|,
∵點A在第二象限,s<0,t>0,
∴![]() ;
;
②∵A(﹣1,![]() ),由①得xB=﹣
),由①得xB=﹣![]() ,
,
∴C(1,![]() ),B(3,
),B(3,![]() ),
),
∴直線OB解析式為:y=![]() x,曲線L在x>時解析式為:y=
x,曲線L在x>時解析式為:y=![]() ,
,
∴直線OB與曲線L在第一象限交點為(![]() ,1),
,1),
∵直線x=n(n>0)交曲線L于G點,交射線AB于點E,交射線OB于點F,
∴G(n,![]() ),E(n,
),E(n,![]() ),F(n,
),F(n,![]() );
);
i)如圖2,當0<n<1時,EF=![]() ,FG=
,FG=![]() ,
,
![]() ,即
,即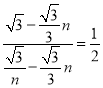 ,解得:n1=3+
,解得:n1=3+![]() (舍去),n2=3﹣
(舍去),n2=3﹣![]() ;
;
ii)如圖3,當1<n<![]() 時,EF>FG,不合題意;
時,EF>FG,不合題意;
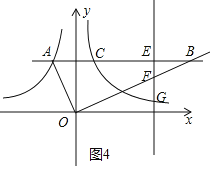
iii)如圖4,當![]() <n<3時,EF=
<n<3時,EF=![]() ,FG=
,FG=![]() ,
,
![]() ,即
,即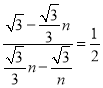 ,解得:n1=1+
,解得:n1=1+![]() ,n2=1﹣
,n2=1﹣![]() (舍去);
(舍去);
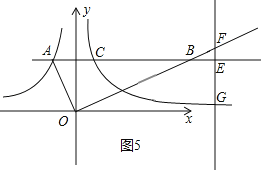
iiii)如圖5,當n>3時,EF=![]() ,FG=
,FG=![]() ,
,
![]() ,即
,即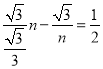 ,解得:n1=3+
,解得:n1=3+![]() ,n2=3﹣
,n2=3﹣![]() (舍去),
(舍去),
綜上所述,當![]() 時,0<n<3﹣
時,0<n<3﹣![]() 或1+
或1+![]() <n<3+
<n<3+![]() .
.



 品學雙優卷系列答案
品學雙優卷系列答案 小學期末沖刺100分系列答案
小學期末沖刺100分系列答案科目:初中數學 來源: 題型:
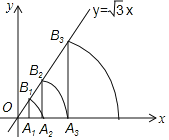
【題目】如圖,直線l:y=![]() x,點A1坐標為(1,0),過點A1作x軸的垂線交直線l于點B1,以原點O為圓心,OB1為半徑畫弧交x軸于點A2;再過點A2作x的垂線交直線l于點B2,以原點O為圓心,OB2長為半徑畫弧交x軸于點A3,…,按此做法進行下去.
x,點A1坐標為(1,0),過點A1作x軸的垂線交直線l于點B1,以原點O為圓心,OB1為半徑畫弧交x軸于點A2;再過點A2作x的垂線交直線l于點B2,以原點O為圓心,OB2長為半徑畫弧交x軸于點A3,…,按此做法進行下去.
求:(1)點B1的坐標和∠A1OB1的度數;
(2)弦A4B3的弦心距的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一袋中裝有形狀大小都相同的四個小球,每個小球上各標有一個數字,分別是1,4,7,8.現規定從袋中任取一個小球,對應的數字作為一個兩位數的個位數;然后將小球放回袋中并攪拌均勻,再任取一個小球,對應的數字作為這個兩位數的十位數.
(1)寫出按上述規定得到所有可能的兩位數;
(2)從這些兩位數中任取一個,求其算術平方根大于4且小于7的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有這樣一個問題:探究函數y=![]() 的圖象與性質.小彤根據學習函數的經驗,對函數y=
的圖象與性質.小彤根據學習函數的經驗,對函數y=![]() 的圖象與性質進行了探究.
的圖象與性質進行了探究.
下面是小彤探究的過程,請補充完整:
(1)函數y=![]() 的自變量x的取值范圍是 ;
的自變量x的取值范圍是 ;
(2)下表是y與x的幾組對應值:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 4 | 5 | 6 | 7 | 8 | … |
y | … |
| m |
| 0 | ﹣1 | 3 | 2 |
|
|
| … |
則m的值為 ;
(3)如圖所示,在平面直角坐標系xOy中,描出了以上表中各對對應值為坐標的點,根據描出的點,畫出了圖象的一部分,請根據剩余的點補全此函數的圖象;
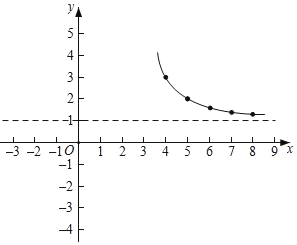
(4)觀察圖象,寫出該函數的一條性質 ;
(5)若函數y=![]() 的圖象上有三個點A(x1,y1)、B(x2,y2)、C(x3,y3),且x1<3<x2<x3,則y1、y2、y3之間的大小關系為 ;
的圖象上有三個點A(x1,y1)、B(x2,y2)、C(x3,y3),且x1<3<x2<x3,則y1、y2、y3之間的大小關系為 ;
查看答案和解析>>
科目:初中數學 來源: 題型:
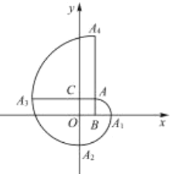
【題目】如圖,在平面直角坐標系中,四邊形![]() 是正方形,點
是正方形,點![]() 的坐標為
的坐標為![]() ,弧
,弧![]() 是以點
是以點![]() 為圓心,
為圓心,![]() 為半徑的圓弧;弧
為半徑的圓弧;弧![]() 是以點
是以點![]() 為圓心,
為圓心,![]() 為半徑的圓弧,弧
為半徑的圓弧,弧![]() 是以點
是以點![]() 為圓心,
為圓心,![]() 為半徑的圓弧,弧
為半徑的圓弧,弧![]() 是以點
是以點![]() 為圓心,
為圓心,![]() 為半徑的圓弧.繼續以點
為半徑的圓弧.繼續以點![]() ,
,![]() ,
,![]() ,
,![]() 為圓心按上述作法得到的曲線
為圓心按上述作法得到的曲線![]() …稱為正方形的“漸開線”,則點
…稱為正方形的“漸開線”,則點![]() 的坐標是__________.
的坐標是__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
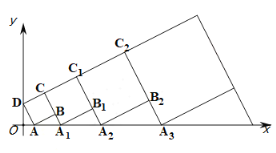
【題目】在平面直角坐標系![]() 中,正方形ABCD的位置如圖所示,點
中,正方形ABCD的位置如圖所示,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,延長
,延長![]() 交
交![]() 軸于點
軸于點![]() ,作正方形
,作正方形![]() ,延長
,延長![]() 交
交![]() 軸于點
軸于點![]() ,作正方形
,作正方形![]() ,…按這樣的規律進行下去,第
,…按這樣的規律進行下去,第![]() 個正方形的面積為_____________.
個正方形的面積為_____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】山西物產豐富,在歷史傳承與現代科技進步中,特色農林牧業、農產品加工業、傳統手工業不斷發展革新,富有地域特色和品牌的士特產品愈加豐富.根據市場調查,下面五種特產比較受人們的青睞:![]() 山西汾酒、
山西汾酒、![]() 山西老陳醋、
山西老陳醋、![]() 晉中平遙牛肉、
晉中平遙牛肉、![]() 山西沁州黃小米、
山西沁州黃小米、![]() 運城芮城麻片,某學校老師帶領學生在集市上隨機調查了部分市民對“我最喜愛的特產”進行投票,將票數進行統計.繪制了如圖所示的條形統計圖和扇形統計圖(均不完整).
運城芮城麻片,某學校老師帶領學生在集市上隨機調查了部分市民對“我最喜愛的特產”進行投票,將票數進行統計.繪制了如圖所示的條形統計圖和扇形統計圖(均不完整).

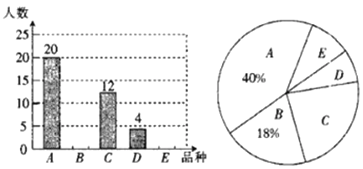
請根據圖中的信息解答下列問題.
![]() 直接寫出參與投票的人數,并補全條形統計圖;
直接寫出參與投票的人數,并補全條形統計圖;
![]() 若該集市上共有
若該集市上共有![]() 人,請估計該集市喜愛運城芮城麻片的人數;
人,請估計該集市喜愛運城芮城麻片的人數;
![]() 若要從這五種特產中隨機抽取出兩種特產,請用畫樹狀圖或列表的方法,求正好抽到山西汾酒和晉中平遙牛肉的概率.
若要從這五種特產中隨機抽取出兩種特產,請用畫樹狀圖或列表的方法,求正好抽到山西汾酒和晉中平遙牛肉的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為響應垃圾分類處理,改善生態環境,某小區將生活垃圾分成三類:廚余垃圾、可回收垃圾和其他垃圾,分別記為a,b,c,并且設置了相應的垃圾箱,“廚余垃圾”箱,“可回收垃圾”箱和“其他垃圾”箱,分別記為A,B,C
(1)小明將垃圾分裝在三個袋中,任意投放,用畫樹狀圖或列表的方法求把三個袋子都放錯位置的概率是多少?
(2)某學習小組為了了解居民生活垃圾分類投放的情況,現隨機抽取了某天三類垃圾箱中總共100噸的生活垃圾,數據統計如表(單位:噸):
A | B | C | |
a | 40 | 10 | 10 |
b | 3 | 24 | 3 |
c | 2 | 2 | 6 |
調查發現,在“可回收垃圾”中塑料類垃圾占10%,每回收1噸塑料類垃圾可獲得0.7噸二級原料,某城市每天大約產生200噸生活垃圾假設該城市每天處理投放正確的垃圾,每天大概可回收多少噸塑料類垃圾的二級原料?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】水城門位于淀浦河和漕港河三叉口,是環城水系公園淀浦河夢蝶島區域重要的標志性景觀.在課外實踐活動中,某校九年級數學興趣小組決定測量該水城門的高.他們的操作方法如下:如圖,先在D處測得點A的仰角為20°,再往水城門的方向前進13米至C處,測得點A的仰角為31°(點D、C、B在一直線上),求該水城門AB的高.(精確到0.1米)
(參考數據:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
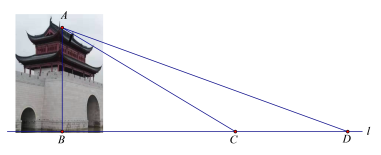
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com