
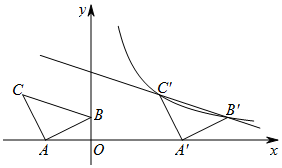
 如圖,在平面直角坐標系中有Rt△ABC,已知∠CAB=90°,AB=AC,A(-2,0),B(0,1).
如圖,在平面直角坐標系中有Rt△ABC,已知∠CAB=90°,AB=AC,A(-2,0),B(0,1).分析 (1)作CN⊥x軸于點N,根據HL證明Rt△CAN≌Rt△AOB,求出NO的長度,進而求出d;
(2)設△ABC沿x軸的正方向平移c個單位,用c表示出C′和B′,根據兩點都在反比例函數圖象上,求出k的值,進而求出c的值,即可求出反比例函數和直線B′C′的解析式;
(3)直接從圖象上找出y1<y2時,x的取值范圍.
解答 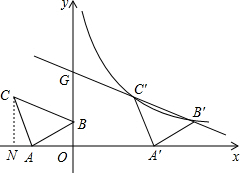 解:(1)作CN⊥x軸于點N,
解:(1)作CN⊥x軸于點N,
∵A(-2,0)B(0,1).
∴OB=1,AO=2,
在Rt△CAN和Rt△AOB,
∵$\left\{\begin{array}{l}{CN=AO}\\{AC=AB}\end{array}\right.$,
∴Rt△CAN≌Rt△AOB(HL),
∴AN=BO=1,CN=AO=2,NO=NA+AO=3,
又∵點C在第二象限,
∴C(-3,2);
(2)設△ABC沿x軸的正方向平移c個單位,
則C′(-3+c,2),則B′(c,1)
又點C′和B′在該比例函數圖象上,
把點C′和B′的坐標分別代入y1=$\frac{k}{x}$,
得-6+2c=c,
解得c=6,
即反比例函數解析式為y1=$\frac{6}{x}$,
(3)此時 C′(3,2),B′(6,1),
設直線B′C′的解析式y2=mx+n,
∵$\left\{\begin{array}{l}{2=3m+n}\\{1=6m+n}\end{array}\right.$,
∴$\left\{\begin{array}{l}{m=-\frac{1}{3}}\\{n=3}\\{\;}\end{array}\right.$,
∴直線C′B′的解析式為y2=-$\frac{1}{3}$x+3;
由圖象可知反比例函數y1和此時的直線B′C′的交點為 C′(3,2),B′(6,1),
∴若y1<y2時,則3<x<6.
點評 本題主要考查了反比例函數的綜合題的知識,解答本題的關鍵是熟練掌握反比例函數的性質以及平移的知識,解決第(2)問關鍵求出c的值,此題難度不是很大.


科目:初中數學 來源: 題型:選擇題
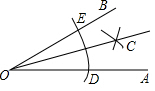 在數學課上,老師用直尺和圓規作角平分線,方法如下:
在數學課上,老師用直尺和圓規作角平分線,方法如下:| A. | SAS | B. | ASA | C. | SSS | D. | AAS |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,已知A,E,F,C在同一條直線上,∠A=∠C,AE=CF,要使△ADF≌△CBE,還需要添加一個條件,這個條件可以是AD=BC(只需寫出一個)
如圖,已知A,E,F,C在同一條直線上,∠A=∠C,AE=CF,要使△ADF≌△CBE,還需要添加一個條件,這個條件可以是AD=BC(只需寫出一個)查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 361×106 | B. | 36.1×107 | C. | 3.61×108 | D. | 0.361×109 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com