
【題目】為了增強學生對新冠病毒預防知識的了解,我校初一年級開展了網上預防知識的宣傳教育活動.為了解這次宣傳教育活動的效果,學校從初一年級1500名學生中隨機抽取部分學生進行網上知識測試(測試滿分100分,得分均為整數),并根據抽取的學生測試成績,制作了如下統(tǒng)計圖表:
抽取學生知識測試成績的頻數表 | ||
成績 | 頻數(人) | 頻率 |
| 10 | 0.1 |
| 15 |
|
|
| 0.2 |
| 40 |
|
|
|
|
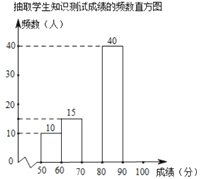
由圖表中給出的信息回答下列問題:
(1)![]() ,
,![]() ,并補全頻數直方圖;
,并補全頻數直方圖;
(2)如果80分以上(包括80分)為優(yōu)秀,請估計初一年級1500名學生中成績優(yōu)秀的人數;
(3)小強在這次測試中成績?yōu)?/span>85分,你認為85分一定是這100名學生知識測試成績的中位數嗎?請簡要說明理由.
【答案】(1)20,15,作圖見解析;(2)825人;(3)不一定,理由見解析.
【解析】
(1)先求解出樣本容量,用樣本容量乘頻率可求得m對應的頻數;在用樣本容量減去50至90分的頻數得n對應的頻數;
(2)先求出優(yōu)秀的比例,再用比例乘總人數即可;
(3)排序后,僅能推斷中位數在![]() 范圍中,不能說明是85分
范圍中,不能說明是85分
(1)樣本容量為:10÷0.1=100人
則m=100×0.2=20
n=100-10-15-20-40=15;
補全頻數直方圖如下:
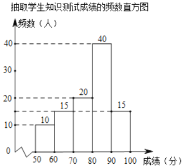
(2)![]() ,
,
答:全校1500名學生中成績優(yōu)秀的人數約為825人;
(3)不一定是,理由:將100名學生知識測試成績從小到大排列,第50、51名的成績都在分數段![]() 中,當他們的平均數不一定是85分.
中,當他們的平均數不一定是85分.


 一線名師提優(yōu)試卷系列答案
一線名師提優(yōu)試卷系列答案 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案科目:初中數學 來源: 題型:
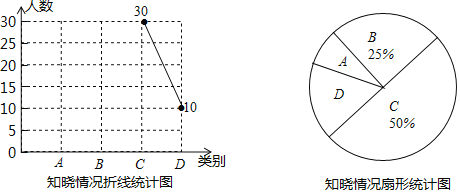
【題目】2018年5月13日,大國重器﹣﹣中國第一艘國產航母正式海試,某校團支部為了了解同學們對此事的知曉情況,隨機抽取了部分同學進行調查,并根據收集到的信息繪制了如下兩幅不完整的統(tǒng)計圖,圖中A表示“知道得很詳細”,B表示“知道個大概”,C表示“聽說了”,D表示“完全不知道”,請根據途中提供的信息完成下列問題:
(1)扇形統(tǒng)計圖中A對應的圓心角是 度,并補全折線統(tǒng)計圖.
(2)被抽取的同學中有4位同學都是班級的信息員,其中有一位信息員屬于D類,校團支部從這4位信息員中隨機選出兩位作為校廣播站某訪談節(jié)目的嘉賓,請用列表法或畫樹狀圖法,求出屬于D類的信息員被選為的嘉賓的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點O是等邊△ABC內一點,∠AOB=110°,∠BOC=a.將△BOC繞點C按順時針方向旋轉60°得△ADC,連接OD.
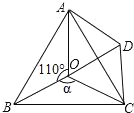
(1)試說明△COD是等邊三角形;
(2)當a=150°時,OB=3,OC=4,試求OA的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在課外實踐中,小明為了測量江中信號塔![]() 離河邊的距離
離河邊的距離![]() ,采取了如下措施:如圖在江邊
,采取了如下措施:如圖在江邊![]() 處,測得信號塔
處,測得信號塔![]() 的俯角為
的俯角為![]() ,若
,若![]() 米,
米,![]() ,
,![]() 米,
米,![]() 平行于
平行于![]() ,
,![]() 的坡度為
的坡度為![]() ,坡長
,坡長![]() 米,則
米,則![]() 的長為( )(精確到0.1米,參考數據:
的長為( )(精確到0.1米,參考數據:![]() ,
,![]() ,
,![]() )
)
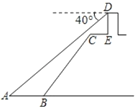
A.78.6米B.78.7米C.78.8米D.78.9米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(問題提出)
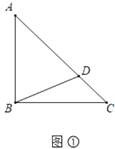
(1)如圖①,在等腰![]() 中,斜邊
中,斜邊![]() ,點
,點![]() 為
為![]() 上一點,連接
上一點,連接![]() ,則
,則![]() 的最小值為 .
的最小值為 .
(問題探究)
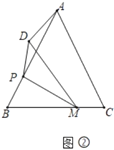
(2)如圖2,在![]() 中,
中,![]() ,
,![]() ,點
,點![]() 是
是![]() 上一點,且
上一點,且![]() ,點
,點![]() 是邊
是邊![]() 上一動點,連接
上一動點,連接![]() ,將
,將![]() 沿
沿![]() 翻折得到
翻折得到![]() ,點
,點![]() 與點
與點![]() 對應,連接
對應,連接![]() ,求
,求![]() 的最小值.
的最小值.
(問題解決)
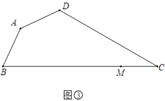
(3)如圖③,四邊形![]() 是規(guī)劃中的休閑廣場示意圖,其中
是規(guī)劃中的休閑廣場示意圖,其中![]() ,
,![]() ,
,![]() ,
,![]() ,點
,點![]() 是
是![]() 上一點,
上一點,![]() .現計劃在四邊形
.現計劃在四邊形![]() 內選取一點
內選取一點![]() ,把
,把![]() 建成商業(yè)活動區(qū),其余部分建成景觀綠化區(qū).為方便進入商業(yè)區(qū),需修建小路
建成商業(yè)活動區(qū),其余部分建成景觀綠化區(qū).為方便進入商業(yè)區(qū),需修建小路![]() 、
、![]() ,從實用和美觀的角度,要求滿足
,從實用和美觀的角度,要求滿足![]() ,且景觀綠化區(qū)面積足夠大,即
,且景觀綠化區(qū)面積足夠大,即![]() 區(qū)域面積盡可能小.則在四邊形
區(qū)域面積盡可能小.則在四邊形![]() 內是否存在這樣的點
內是否存在這樣的點![]() ?若存在,請求出
?若存在,請求出![]() 面積的最小值;若不存在,請說明理由.
面積的最小值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y = ![]() ax2 ax + c圖象的頂點為C,一次函數y = x + 3的圖象與這個二次函數的圖象交于A、B兩點(其中點A在點B的左側),與它的對稱軸交于點D.
ax2 ax + c圖象的頂點為C,一次函數y = x + 3的圖象與這個二次函數的圖象交于A、B兩點(其中點A在點B的左側),與它的對稱軸交于點D.
(1)求點D的坐標;
(2) ①若點C與點D關于x軸對稱,且△BCD的面積等于4,求此二次函數的關系式;
②若CD=DB,且△BCD的面積等于4![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
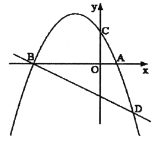
【題目】如圖,已知拋物線![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點,與
兩點,與![]() 軸交于
軸交于![]() 點,直線
點,直線![]() 交拋物線于點
交拋物線于點![]() ,并且,
,并且,![]() ,
,![]() .
.
(1)求拋物線的解析式;
(2)已知點![]() 為拋物線上一動點,且在第二象限,順次連接點
為拋物線上一動點,且在第二象限,順次連接點![]() 、
、![]() 、
、![]() 、
、![]() ,求四邊形
,求四邊形![]() 面積的最大值;
面積的最大值;
(3)在(2)中四邊形![]() 面積最大的條件下,過點
面積最大的條件下,過點![]() 作直線平行于
作直線平行于![]() 軸,在這條直線上是否存在一個以
軸,在這條直線上是否存在一個以![]() 點為圓心,
點為圓心,![]() 為半徑且與直線
為半徑且與直線![]() 相切的圓?若存在,求出圓心
相切的圓?若存在,求出圓心![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知直線y1=﹣x+2和拋物線![]() 相交于點A,B.
相交于點A,B.
(1)當k=![]() 時,求兩函數圖象的交點坐標;
時,求兩函數圖象的交點坐標;
(2)二次函數y2的頂點為P,PA或PB與直線y1=﹣x+2垂直時,求k的值.
(3)當﹣4<x<2時,y1>y2,試直接寫出k的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com