
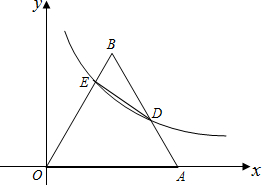
 如圖,等邊△ABO在平面直角坐標系中,點A的坐標為(4,0),反比例函數y=$\frac{k}{x}$(x>0,k≠0)的圖象經過AB的中點D,交OB于E.
如圖,等邊△ABO在平面直角坐標系中,點A的坐標為(4,0),反比例函數y=$\frac{k}{x}$(x>0,k≠0)的圖象經過AB的中點D,交OB于E.分析 (1)過點B作BC⊥x軸于點C,則OC=AC=2,根據等邊三角形的性質求得OC和BC的長,得到點B的坐標,然后根據待定系數法求得直線OB的解析式;根據中點的性質求得AB的中點D的坐標,代入y=$\frac{k}{x}$,即可求得k的值;
(2)先將直線OB的解析式與反比例函數的解析式聯立求出E點坐標,求出BE、BD的長,再作EF⊥BD于F,求出EF,然后根據三角形面積公式求解即可.
解答 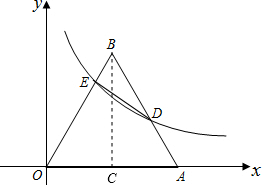 解:(1)過點B作BC⊥x軸于點C,
解:(1)過點B作BC⊥x軸于點C,
∵△ABO是等邊三角形,點A的坐標為(4,0),
∴OC=AC=2.
由勾股定理得:BC=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴B(2,2$\sqrt{3}$),
設直線OB的函數解析式為y=mx,則2$\sqrt{3}$=2m,
∴m=$\sqrt{3}$.
∴直線OB的函數解析式為y=$\sqrt{3}$x;
∵D為AB的中點,
∴D(3,$\sqrt{3}$),
∴k=3$\sqrt{3}$; (2)將y=$\sqrt{3}$x代入y=$\frac{3\sqrt{3}}{x}$,得$\sqrt{3}$x=$\frac{3\sqrt{3}}{x}$,
(2)將y=$\sqrt{3}$x代入y=$\frac{3\sqrt{3}}{x}$,得$\sqrt{3}$x=$\frac{3\sqrt{3}}{x}$,
解得x=±$\sqrt{3}$(負值舍去),
則E($\sqrt{3}$,3),
∵B(2,2$\sqrt{3}$),D(3,$\sqrt{3}$),
∴BE=$\sqrt{(2-\sqrt{3})^{2}+(2\sqrt{3}-3)^{2}}$=4-2$\sqrt{3}$,BD=$\frac{1}{2}$AB=$\frac{1}{2}$OA=2.
如圖,作EF⊥BD于F,則EF=BE•sin∠B=(4-2$\sqrt{3}$)×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$-3,
∴△BDE的面積=$\frac{1}{2}$BD•EF=$\frac{1}{2}$×2×(2$\sqrt{3}$-3)=2$\sqrt{3}$-3.
點評 本題考查了反比例函數與一次函數的交點問題:求反比例函數與一次函數的交點坐標,把兩個函數關系式聯立成方程組求解,若方程組有解則兩者有交點,方程組無解,則兩者無交點.也考查了等邊三角形的性質,勾股定理,三角形的面積.利用待定系數法求出函數的解析式是解題的關鍵.


 孟建平錯題本系列答案
孟建平錯題本系列答案 超能學典應用題題卡系列答案
超能學典應用題題卡系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
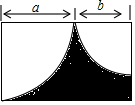 如圖所示,用含a、b字母的代數式表示圖中陰影部分的面積為${a}^{2}+ab-\frac{π{a}^{2}}{4}-\frac{π{b}^{2}}{4}$.
如圖所示,用含a、b字母的代數式表示圖中陰影部分的面積為${a}^{2}+ab-\frac{π{a}^{2}}{4}-\frac{π{b}^{2}}{4}$.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,有兩條公路OM,ON相交成30°角.沿公路OM方向離O點80米處有一所學校A,當重型運輸卡車P沿道路ON方向行駛時,在以P為圓心50米長為半徑的圓形區域內都會受到卡車噪聲的影響,且卡車P與學校A的距離越近噪聲影響越大.若已知重型運輸卡車P沿道路ON方向行駛的速度為18千米/時.
如圖,有兩條公路OM,ON相交成30°角.沿公路OM方向離O點80米處有一所學校A,當重型運輸卡車P沿道路ON方向行駛時,在以P為圓心50米長為半徑的圓形區域內都會受到卡車噪聲的影響,且卡車P與學校A的距離越近噪聲影響越大.若已知重型運輸卡車P沿道路ON方向行駛的速度為18千米/時.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com