
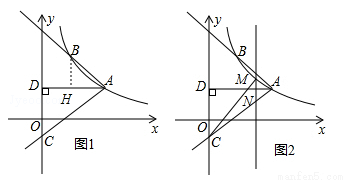
(本題滿分13分)如圖1,反比例函數 (
( )的圖象經過點A(
)的圖象經過點A( ,1),射線AB與反比例函數圖象交與另一點B(1,
,1),射線AB與反比例函數圖象交與另一點B(1, ),射線AC與
),射線AC與 軸交于點C,∠BAC=75°,AD⊥y軸,垂足為D.
軸交于點C,∠BAC=75°,AD⊥y軸,垂足為D.


(1)求 的值;
的值;
(2)求∠DAC的度數及直線AC的解析式;
(3)如圖2,M是線段AC上方反比例函數圖象上一動點,過M作直線 軸,與AC相交于N,連接CM,求△CMN面積的最大值.
軸,與AC相交于N,連接CM,求△CMN面積的最大值.
(1)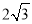 ;(2)30°,
;(2)30°,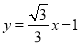 ;(3)
;(3)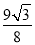 .
.
【解析】
試題分析:(1)根據反比例函數圖象上點的坐標特征易得k=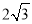 ;
;
(2)作BH⊥AD于H,如圖1,根據反比例函數圖象上點的坐標特征確定B點坐標為(1,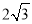 ),則AH=
),則AH=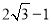 ,BH=
,BH=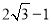 ,可判斷△ABH為等腰直角三角形,所以∠BAH=45°,得到∠DAC=∠BAC﹣∠BAH=30°,根據特殊角的三角函數值得tan∠DAC=
,可判斷△ABH為等腰直角三角形,所以∠BAH=45°,得到∠DAC=∠BAC﹣∠BAH=30°,根據特殊角的三角函數值得tan∠DAC=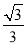 ;由于AD⊥y軸,則OD=1,AD=
;由于AD⊥y軸,則OD=1,AD=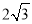 ,然后在Rt△OAD中利用正切的定義可計算出CD=2,易得C點坐標為(0,﹣1),于是可根據待定系數法求出直線AC的解析式為
,然后在Rt△OAD中利用正切的定義可計算出CD=2,易得C點坐標為(0,﹣1),于是可根據待定系數法求出直線AC的解析式為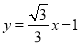 ;
;
(3)利用M點在反比例函數圖象上,可設M點坐標為(t,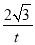 )(0<t<1),由于直線l⊥x軸,與AC相交于點N,得到N點的橫坐標為t,利用一次函數圖象上點的坐標特征得到N點坐標為(t,
)(0<t<1),由于直線l⊥x軸,與AC相交于點N,得到N點的橫坐標為t,利用一次函數圖象上點的坐標特征得到N點坐標為(t,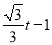 ),則MN=
),則MN=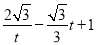 ,根據三角形面積公式得到
,根據三角形面積公式得到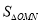 =
=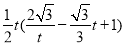 ,再進行配方得到S=
,再進行配方得到S=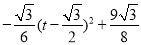 (0<t<1),最后根據二次函數的最值問題求解.
(0<t<1),最后根據二次函數的最值問題求解.
試題解析:(1)把A(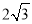 ,1)代入
,1)代入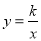 ,得
,得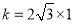 =
=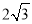 ;
;
(2)作BH⊥AD于H,如圖1,把B(1,a)代入反比例函數解析式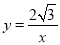 ,得a=
,得a=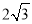 ,∴B點坐標為(1,
,∴B點坐標為(1,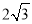 ),∴AH=
),∴AH=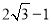 ,BH=
,BH=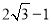 ,∴△ABH為等腰直角三角形,∴∠BAH=45°,∵∠BAC=75°,∴∠DAC=∠BAC﹣∠BAH=30°,∴tan∠DAC=tan30°=
,∴△ABH為等腰直角三角形,∴∠BAH=45°,∵∠BAC=75°,∴∠DAC=∠BAC﹣∠BAH=30°,∴tan∠DAC=tan30°=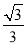 ,∵AD⊥y軸,∴OD=1,AD=
,∵AD⊥y軸,∴OD=1,AD=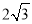 ,∵tan∠DAC=
,∵tan∠DAC=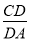 =
=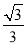 ,∴CD=2,∴OC=1,∴C點坐標為(0,﹣1),設直線AC的解析式為
,∴CD=2,∴OC=1,∴C點坐標為(0,﹣1),設直線AC的解析式為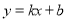 ,把A(
,把A(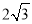 ,1)、C(0,﹣1)代入,得:
,1)、C(0,﹣1)代入,得: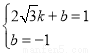 ,解得:
,解得: ,∴直線AC的解析式為
,∴直線AC的解析式為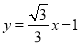 ;
;
(3)設M點坐標為(t,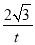 )(0<t<1),∵直線l⊥x軸,與AC相交于點N,∴N點的橫坐標為t,∴N點坐標為(
)(0<t<1),∵直線l⊥x軸,與AC相交于點N,∴N點的橫坐標為t,∴N點坐標為(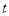 ,
,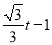 ),∴MN=
),∴MN=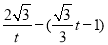 =
=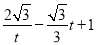 ,
,
∴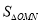 =
=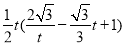 =
=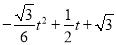 =
=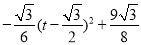 (0<t<1),
(0<t<1),
∵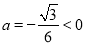 ,∴當
,∴當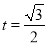 時,S有最大值,最大值為
時,S有最大值,最大值為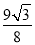 .
.
考點:1.反比例函數綜合題;2.一次函數的性質;3.二次函數的最值.


科目:初中數學 來源: 題型:解答題
如圖,圓心角都是90°的扇形OAB與扇形OCD疊放在-起,連接AC、BD。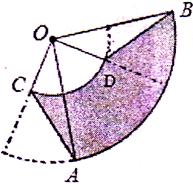
(1)AC與BD相等嗎?為什么?
(2)若0A=2cm,OC=lcm,求圖中陰影部分的面積。
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省九年級上學期期中調研考試數學試卷(解析版) 題型:解答題
(本題滿分10分)如圖,AB是⊙O的直徑,弦DE垂直平分半徑OA,C為垂足,弦DF與半徑OB相交于點P,連結EF、EO,若DE= ,∠DPA=45°.
,∠DPA=45°.

(1)求⊙O的半徑;
(2)求圖中陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省九年級上學期期中考試數學試卷(解析版) 題型:解答題
(10分)如圖,在△ABC中,AC=BC,AB是⊙C的切線,切點為D,直線AC交⊙C于點E、F,且CF= AC.
AC.

(1)求∠ACB的度數;
(2)若AC=8,求△ABF的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com