
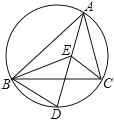
【題目】如圖,點 E 是△ABC 的內心,AE 的延長線和△ABC 的外接圓相交于點 D,連 接 BE
(1) 若∠CBD=35°,求∠BAC 及∠BEC 的度數
(2) 求證:DE=DB
【答案】(1) 125°;(2)見詳解.
【解析】
(1)根據三角形的內心是三條角平分線的交點,得到∠BAC=2∠CAD,∠ABC=2∠EBC,∠ACB=∠ECB,再用三角形內角和求出∠BEC;
(2)由三角形的內心E得到∠BAD=∠CAD,∠EBA=∠EBC,經過等量代換得∠DEB=∠DBE,所以DE=DB.
(1)在外接圓中,∵∠CBD=35°,
∵∠CAD=35°,
∵點E是△ABC的內心,
∴∠BAC=2∠CAD =70°,
∴∠EBC+∠ECB=(180°-70°)÷2=55°,
∴∠BEC=180°-55°=125°.
(2) 證明:∵E是△ABC的內心,
∴∠BAD=∠CAD,∠EBA=∠EBC,
∵∠DEB=∠BAD +∠EBA,∠DBE=∠EBC +∠CBD,∠CBD =∠CAD,
∴∠DEB=∠DBE,
∴DE=DB.


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案科目:初中數學 來源: 題型:
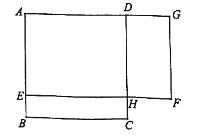
【題目】如圖, ![]() 是一塊邊長為4米的正方形苗圃,園林部門將其改造為矩形
是一塊邊長為4米的正方形苗圃,園林部門將其改造為矩形![]() 的形狀,其中點
的形狀,其中點![]() 在
在![]() 邊上,點
邊上,點![]() 在
在![]() 的延長線上,
的延長線上, ![]() 設
設![]() 的長為
的長為![]() 米,改造后苗圃
米,改造后苗圃![]() 的面積為
的面積為![]() 平方米.
平方米.
(1) ![]() 與
與![]() 之間的函數關系式為 (不需寫自變量的取值范圍);
之間的函數關系式為 (不需寫自變量的取值范圍);
(2)根據改造方案,改造后的矩形苗圃![]() 的面積與原正方形苗圃
的面積與原正方形苗圃![]() 的面積相等,請問此時
的面積相等,請問此時![]() 的長為多少米?
的長為多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
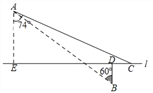
【題目】如圖,在航線l的兩側分別有觀測點A和B,點B到航線l的距離BD為4km,點A位于點B北偏西60°方向且與B相距20km處.現有一艘輪船從位于點A南偏東74°方向的C處,沿該航線自東向西航行至觀測點A的正南方向E處.求這艘輪船的航行路程CE的長度.(結果精確到0.1km)(參考數據:![]() ≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程ax2+bx=0 (a≠0)的一個根是x=2018,,則方程a(x+2)2+bx+2b=0的根是___________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于平面直角坐標系![]() O
O![]() 中的點P和⊙C,給出如下定義:若⊙C上存在兩個點M,N,使得∠MPN=60°,則稱P為⊙C 的關聯點。已知點D(
中的點P和⊙C,給出如下定義:若⊙C上存在兩個點M,N,使得∠MPN=60°,則稱P為⊙C 的關聯點。已知點D(![]() ,
,![]() ),E(0,-2),F(
),E(0,-2),F(![]() ,0)
,0)
(1)當⊙O的半徑為1時,
①在點O,D,E,F中,⊙O的關聯點是______ ____;
②如果G(0,t)是⊙O的關聯點,則t的取值范圍是 ;
(2)如果線段EF上每一個點都是⊙O的關聯點,那么⊙O的半徑![]() 最小為 ;
最小為 ;
(3)Rt⊿ABC中,∠C=90![]() ,BC=8,∠A=30
,BC=8,∠A=30![]() ,⊙P的半徑為1,當點P運動時,始終確保⊿ABC的三條邊中至少有一條邊上恰好有唯一的⊙P的關聯點。請你畫出點P所走過的路線圍成的圖形的示意圖,并在下面橫線上直接寫出它的總長。
,⊙P的半徑為1,當點P運動時,始終確保⊿ABC的三條邊中至少有一條邊上恰好有唯一的⊙P的關聯點。請你畫出點P所走過的路線圍成的圖形的示意圖,并在下面橫線上直接寫出它的總長。

答:點P經過的路線圍成的圖形的總長為 。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程x2+(2m+1)x+m2﹣2=0.
(1)若該方程有兩個實數根,求m的最小整數值;
(2)若方程的兩個實數根為x1,x2,且(x1﹣x2)2+m2=21,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場試銷一種成本為60元/件的T恤,規定試銷期間單價不低于成本單價,又獲利不得高于40%,經試銷發現,銷售量y(件)與銷售單價x(元/件)符合一次函數y=kx+b,且x=70時,y=50;x=80時,y=40;
(1)求出一次函數y=kx+b的解析式
(2)若該商場獲得利潤為w元,試寫出利潤w與銷售單價x之間的關系式,銷售單價定為多少時,商場可獲得最大利潤,最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
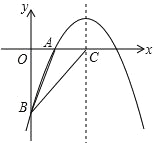
【題目】如圖,二次函數 y=﹣x2+bx+c 的圖象經過 A(1,0),B(0,﹣3)兩點.
(1)求這個拋物線的解析式及頂點坐標;
(2)設該二次函數的對稱軸與 x 軸交于點 C,連接 BA、BC,求△ABC 的面積.
(3)在拋物線的對稱軸上是否存在一點 P,使得 O、B、C、P 四點為頂點的四邊形是平行四邊形?若存在,請直接寫出 P 點坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com