
分析 分x≥0和x<0兩種情況考慮,利用配方法解一元二次方程可求出x的值,再根據(jù)方程x2-2|x|+k=0有2個不相等的根,即可得出關(guān)于k的一元一次不等式組,解之即可得出結(jié)論.
解答 解:當x≥0時,原方程為x2-2x+k=(x-1)2+k-1=0,
解得:x1=1-$\sqrt{1-k}$,x2=1+$\sqrt{1-k}$(1-k≥0);
當x<0時,原方程為x2+2x+k=(x+1)2+k-1=0,
解得:x3=-1-$\sqrt{1-k}$,x4=-1+$\sqrt{1-k}$(1-k≥0).
∵方程x2-2|x|+k=0有2個不相等的根,
∴$\left\{\begin{array}{l}{1-k≥0}\\{1-\sqrt{1-k}<0}\\{-1+\sqrt{1-k}≥0}\end{array}\right.$,
解得:k<0.
∴若方程x2-2|x|+k=0有2個不相等的根,k的取值范圍為k<0.
點評 本題考查了配方法解一元二次方程以及解一元一次不等式組,利用配方法求出方程的根結(jié)合方程有兩個不等的根找出關(guān)于k的一元一次不等式組是解題的關(guān)鍵.


 期末沖刺100分創(chuàng)新金卷完全試卷系列答案
期末沖刺100分創(chuàng)新金卷完全試卷系列答案科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 以上都不對 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | abc2與3bac2 | B. | 2an2與-a2n | C. | 5與-2x | D. | -$\frac{1}{3}$a2y與$\frac{2}{3}$a2 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
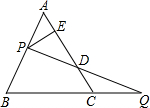 如圖,過邊長為1的等邊△ABC的邊AB上一點P,作PE⊥AC于E,Q為BC延長線上一點,當PA=CQ時,連PQ交AC邊于D,則DE的長為( )
如圖,過邊長為1的等邊△ABC的邊AB上一點P,作PE⊥AC于E,Q為BC延長線上一點,當PA=CQ時,連PQ交AC邊于D,則DE的長為( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | (3,0) | B. | (3,-3) | C. | (3,-1) | D. | (-1,3) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 0.287×1010美元 | B. | 0.287×1011美元 | C. | 2.87×1010美元 | D. | 2.87×1011美元 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com