Question

等腰Rt△ABC中，∠BAC=90°，點A、點B分別是x軸、y軸兩個動點，直角邊AC交x軸于點D，斜邊BC交y軸于點E。
（1）如圖（1），若A(0，1)，B(2，0)，求C點的坐標；
（2）如圖（2）， 當等腰Rt△ABC運動到使點D恰為AC中點時，連接DE，求證：∠ADB=∠CDE；
（3）如圖（3），在等腰Rt△ABC不斷運動的過程中，若滿足BD始終是∠ABC的平分線，試探究：線段OA、OD、BD三者之間是否存在某一固定的數量關系，并說明理由。

Answer 1

（1）C(－1，－1)；（2）見解析；（3）BD="2(OA" +OD)

試題分析：（1）過點C作CF⊥y軸于點F，則△ACF≌△ABO(AAS)，即得CF=OA=1，AF=OB=2，
從而求得結果；
（2）過點C作CG⊥AC交y軸于點G，則△ACG≌△ABD(ASA)，即得CG=AD=CD，∠ADB=∠G， 由∠DCE=∠GCE=45°，可證△DCE≌△GCE(SAS)得∠CDE=∠G，從而得到結論；
(3)在OB上截取OH=OD，連接AH，由對稱性得AD="AH," ∠ADH=∠AHD，可得∠AHD=∠ADH=∠BAO=∠BEO，即得∠AEC=∠BHA，從而證得△ACE≌△BAH(AAS)，即可得到   AE=BH=2OA，從而得到結果.
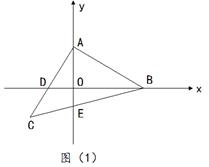
（1）如圖，過點C作CF⊥y軸于點F

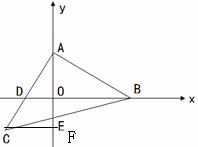
則△ACF≌△ABO(AAS)，
∴CF=OA=1，AF=OB=2
∴OF=1
∴C(－1，－1)；
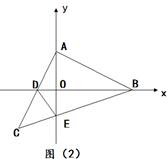
（2）如圖，過點C作CG⊥AC交y軸于點G

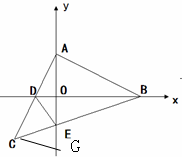
則△ACG≌△ABD(ASA)
∴CG=AD=CD，∠ADB="∠G"
∵∠DCE=∠GCE=45°
∴△DCE≌△GCE(SAS)
∴∠CDE=∠G
∴∠ADB=∠CDE；  
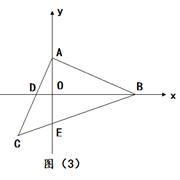
(3) 如圖，在OB上截取OH=OD，連接AH

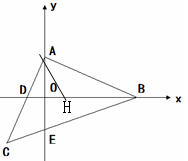
由對稱性得AD="AH," ∠ADH=∠AHD
∴∠AHD=∠ADH=∠BAO=∠BEO
∴∠AEC=∠BHA    
又∵AB=AC  ∠CAE=∠ABH
∴△ACE≌△BAH(AAS)   
∴AE=BH=2OA        
∵DH=2OD
∴BD="2(OA" +OD)
點評：解答本題的關鍵是正確作出輔助線，同時熟練掌握全等三角形的判定方法，靈活選擇恰當的三角形進行分析.