
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以點
,以點![]() 為圓心,以
為圓心,以![]() 為半徑作優弧
為半徑作優弧![]() ,交
,交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() .點
.點![]() 在優弧
在優弧![]() 上從點
上從點![]() 開始移動,到達點
開始移動,到達點![]() 時停止,連接
時停止,連接![]() .
.
(1)當![]() 時,判斷
時,判斷![]() 與優弧
與優弧![]() 的位置關系,并加以證明;
的位置關系,并加以證明;
(2)當![]() 時,求點
時,求點![]() 在優弧
在優弧![]() 上移動的路線長及線段
上移動的路線長及線段![]() 的長.
的長.
(3)連接![]() ,設
,設![]() 的面積為
的面積為![]() ,直接寫出
,直接寫出![]() 的取值范圍.
的取值范圍.
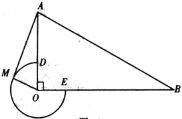
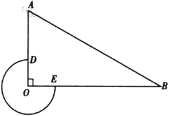
備用圖
【答案】(1)AM與優弧的相切(2)![]() 或
或![]() (3)
(3)![]()
【解析】
(1)根據勾股定理的得到∠AMO=90°即可得到![]() 與優弧
與優弧![]() 的相切;
的相切;
(2)根據題意分![]() 在直線
在直線![]() 的左側和右側兩種情況討論,用三角函數及相似三角形的性質進行求解;(3)根據題意作過點
的左側和右側兩種情況討論,用三角函數及相似三角形的性質進行求解;(3)根據題意作過點![]() 作
作![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() 此時
此時![]() 的面積最大,過點
的面積最大,過點![]() 作
作![]() 于點
于點![]() ,即點
,即點![]() 與點
與點![]() 重合,此時
重合,此時![]() 的面積最小,分別求出
的面積最小,分別求出![]() 最大值與最小值即可求解.
最大值與最小值即可求解.
在![]() 中,
中,![]() ,
,![]() ,
,![]()
![]() .
.
(1)![]() 與優弧的相切;
與優弧的相切;
如圖1,當![]() 時,
時,![]() ,
,![]() 且
且![]()
![]() 為直角三角形,
為直角三角形,![]() ,
,
![]() 點
點![]() 在
在![]() 上,
上,![]()
![]() 與優弧
與優弧![]() 的相切.
的相切.
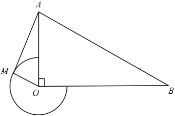
(2)當![]() 時,第一種情況:如圖 2所示,
時,第一種情況:如圖 2所示,![]() 在直線
在直線![]() 的左側;
的左側;![]()
![]()
過點![]() 作
作![]() 于點
于點![]()
在![]() 中,
中,![]()
![]() ,
,![]() ,
,![]()
在![]() 中,據勾股定理可知
中,據勾股定理可知![]() .
.
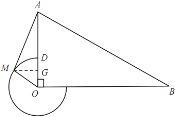
第二種情況:如圖 3所示,![]() 在直線
在直線![]() 的右側;連接
的右側;連接![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
在![]() 中,據勾股定理得:
中,據勾股定理得:![]()
由![]() 可知
可知![]() .
.

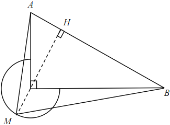
(3)如圖4,過點![]() 作
作![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() 此時
此時![]() 的面積最大
的面積最大
在![]() 中,
中,![]() ,
,![]()
![]()
![]()
在![]() 中
中![]()
![]()
![]()
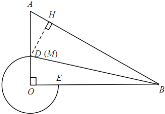
如圖5,過點![]() 作
作![]() 于點
于點![]() ,即點
,即點![]() 與點
與點![]() 重合,此時
重合,此時![]() 的面積最小
的面積最小
在![]() 中
中
![]()
![]()
![]() .
.


 贏在課堂名師課時計劃系列答案
贏在課堂名師課時計劃系列答案 天天向上課時同步訓練系列答案
天天向上課時同步訓練系列答案科目:初中數學 來源: 題型:
【題目】綠色無公害蔬菜基地有甲、乙兩種植戶,他們種植了![]() 兩類蔬菜,兩種植戶種植的兩類蔬菜的種植面積與總收入如下表:
兩類蔬菜,兩種植戶種植的兩類蔬菜的種植面積與總收入如下表:
種植戶 | 種植 | 種植 | 總收入(單位:元) |
甲 |
|
|
|
乙 |
|
|
|
說明:不同種植戶種植的同類蔬菜每畝的平均收入相等;畝為土地面積單位
![]() 求
求![]() 兩類蔬菜每畝的平均收入各是多少元?
兩類蔬菜每畝的平均收入各是多少元?
![]() 某種植戶準備租
某種植戶準備租![]() 畝地用來種植
畝地用來種植![]() 兩類蔬菜,為了使總收入不低于
兩類蔬菜,為了使總收入不低于![]() 元且種植
元且種植![]() 類蔬菜的面積多于種植
類蔬菜的面積多于種植![]() 類蔬菜的面積(兩類蔬菜的種植面積均為整數),求該種植戶所有租地方案;
類蔬菜的面積(兩類蔬菜的種植面積均為整數),求該種植戶所有租地方案;
![]() 在
在![]() 的基礎上,指出哪種方案使總收入最大,并求出最大值.
的基礎上,指出哪種方案使總收入最大,并求出最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“最美女教師”張麗莉,為搶救兩名學生,以致雙腿高位截肢,社會各界紛紛為她捐款,我市某中學九年級一班全體同學參加了捐款活動,該班同學捐款情況的部分統計圖如圖所示:

(1)求該班的總人數;
(2)將條形圖補充完整,并寫出捐款總額的眾數;
(3)該班平均每人捐款多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC與△DEF都是等腰三角形,且AB=AC=3,DE=DF=2,若∠B+∠E=90°,則△ABC與△DEF的面積比為( )

A、9:4 B、3:2 C、![]() :
:![]() D、3
D、3![]() :2
:2![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,點
中,點![]() 坐標是
坐標是![]() .當把坐標系繞點
.當把坐標系繞點![]() 順時針選擇30°時,點
順時針選擇30°時,點![]() 在旋轉后的坐標系中的坐標是____;當把坐標系繞點
在旋轉后的坐標系中的坐標是____;當把坐標系繞點![]() 逆時針選擇30°時,點
逆時針選擇30°時,點![]() 在旋轉后的坐標系中的坐標是____.
在旋轉后的坐標系中的坐標是____.
查看答案和解析>>
科目:初中數學 來源: 題型:
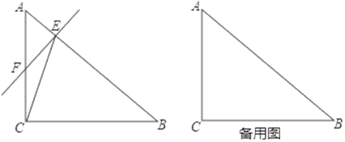
【題目】如圖,在△ABC中,∠ACB=90°,AC=6,BC=8,動點E從點A出發沿著線段AB向終點B運動,速度為每秒3個單位長度,過點E作EF⊥AB交直線AC于點F,連結CE.設點E的運動時間為t秒.
(1)當點F在線段AC上(不含端點)時,
①求證:△ABC∽△AFE;
②當t為何值時,△CEF的面積為1.2;
(2)在運動過程中,是否存在某時刻t,使△CEF為等腰三角形?若存在,求出t的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
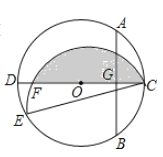
【題目】如圖,CD是⊙O的直徑,AB是⊙O的弦,AB⊥CD,垂足為G,OG:OC=3:5,AB=8.點E為圓上一點,∠ECD=15°,將![]() 沿弦CE翻折,交CD于點F,圖中陰影部分的面積=_________
沿弦CE翻折,交CD于點F,圖中陰影部分的面積=_________
查看答案和解析>>
科目:初中數學 來源: 題型:
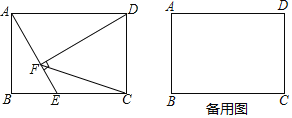
【題目】如圖,在矩形ABCD中,AB=4,BC=5,E是BC邊上的一個動點,DF⊥AE,垂足為點F,連結CF
(1)若AE=BC
①求證:△ABE≌△DFA;②求四邊形CDFE的周長;③求tan∠FCE的值;
(2)探究:當BE為何值時,△CDF是等腰三角形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com