
如圖,在Rt△ABC中,∠C=90°,AC=8cm,BC=6CM.點P,Q同時由B,A兩點出發,分別沿射線BC,AC方向以1cm/s的速度勻速運動.
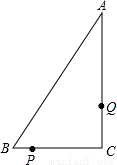
(1)幾秒后△PCQ的面積是△ABC面積的一半?
(2)連結BQ,幾秒后△BPQ是等腰三角形?
(1)2秒或12秒時△PCQ的面積等于△ABC的面積的一半.(2)t=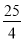 、12或14±4
、12或14±4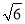 時,△BPQ是等腰三角形.
時,△BPQ是等腰三角形.
【解析】
試題分析:(1)設P、Q同時出發,x秒鐘后,當0<x<6時,當6<x<8時,當x>8時,由此等量關系列出方程求出符合題意的值;
(2)分別根據①當BP=BQ時,②當PQ=BQ時,③當BP=PQ時,利用勾股定理求出即可.
試題解析:(1)設運動x秒后,△PCQ的面積是△ABC面積的一半,
當0<x<6時,
S△ABC=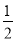 ×AC•BC=
×AC•BC=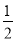 ×6×8=24,
×6×8=24,
即: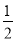 ×(8-x)×(6-x)=
×(8-x)×(6-x)=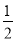 ×24,
×24,
x2-14x+24=0,
(x-2)(x-12)=0,
x1=12(舍去),x2=2;
當6<x<8時,
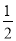 ×(8-x)×(x-6)=
×(8-x)×(x-6)=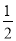 ×24,
×24,
x2-14x+72=0,
b2-4ac=196-288=-92<0,
∴此方程無實數根,
當x>8時,
S△ABC=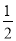 ×AC•BC=
×AC•BC=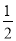 ×6×8=24,
×6×8=24,
即: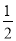 ×(x-8)×(x-6)=
×(x-8)×(x-6)=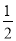 ×24,
×24,
x2-14x+24=0,
(x-2)(x-12)=0,
x1=12,x2=2(舍去),
所以,當2秒或12秒時使得△PCQ的面積等于△ABC的面積的一半.
(2)設t秒后△BPQ是等腰三角形,
①當BP=BQ時,t2=62+(8-t)2,
解得:t=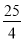 ;
;
②當PQ=BQ時,(6-t)2+(8-t)2=62+(8-t)2,
解得:t=12;
③當BP=PQ時,t2=(6-t)2+(8-t)2,
解得:t=14±4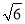 .
.
所以:當t=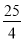 、12或14±4
、12或14±4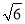 時,△BPQ是等腰三角形.
時,△BPQ是等腰三角形.
考點:一元二次方程的應用.


 培優口算題卡系列答案
培優口算題卡系列答案 開心口算題卡系列答案
開心口算題卡系列答案科目:初中數學 來源:2014-2015學年四川省涼山州九年級上學期期末數學試卷(解析版) 題型:選擇題
將一元二次方程5x2-1=4x化成一般形式后,二次項系數和一次項系數分別是( )
A.5 -1 B.5 4 C.5 -4 D.5x 4x
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山東省泰安市九年級第二次月考數學試卷(解析版) 題型:選擇題
將拋物線y= (x -1)2 +3向左平移1個單位,再向下平移3個單位后所得拋物線的解析式為( )
A.y=(x -2)2 B.y=(x -2)2+6 C.y=x2+6 D.y=x2
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山東省泰安市九年級第二次月考數學試卷(解析版) 題型:選擇題
對于任意實數k,關于x的方程程x2-2(k+1)x-k2+2k-1=0的根的情況為
A.有兩個相等的實數根 B.沒有實數根
C.有兩個不相等的實數根 D.無法確定
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山東省膠南市九年級上學期第一次月考數學試卷(解析版) 題型:解答題
解方程:(1)2t2-6t+3=0(用配方法);
(2)3(x-5)2=2(5-x)(用因式分解法)
(3)2x2-4x-1=0(公式法)
(4)2x2+1= (公式法)
(公式法)
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山東省膠南市九年級上學期第一次月考數學試卷(解析版) 題型:填空題
如圖,已知AB=AC,∠A=440,AB的垂直平分線MN交AC于點D,則∠DBC= 。
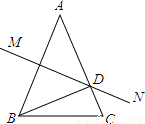
查看答案和解析>>
科目:初中數學 來源:2014-2015學年內蒙古赤峰市寧城縣八年級上學期期末考試數學試卷(解析版) 題型:解答題
(本題滿分8分)如圖,在四邊形ABCD中,AD∥BC,E是AB的中點,連接DE并延長交CB的延長線于點F,點G在BC邊上,且∠GDF=∠ADF.
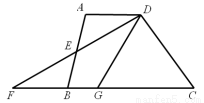
(1)求證:△ADE≌△BFE;
(2)連接EG,判斷EG與DF的位置關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年遼寧省七年級上學期三科聯賽數學試卷(解析版) 題型:選擇題
關于x的方程4m-3x=1的解為-1,那么m應取( )
A、1 B、-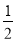 C、-1 D、-2
C、-1 D、-2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com