
分析 觀察題中已知:是從1開始的奇數求和,結果為自然數的平方,若算式的最后一個為2n+1,結果恰是(n+1)2,由此可以求解.
解答 解:已知是從1開始的奇數求和,結果為自然數的平方,若算式的最后一個為2n+1,結果恰是(n+1)2;
1+3+5+7+9+…+13=72=49;
1+3+5+7+9+…+(2n-1)+(2n+1)=(n+1)2;
41+43+45+…+77+79=1+3+5+7+9+…+77+79-(1+3+5+7+9+…+39)=402-202=1200.
故答案為:49,(n+1)2,1200.
點評 此題主要考查數列的規律探索與運用,觀察已知找到存在的規律,并準確應用是解題的關鍵.


科目:初中數學 來源: 題型:選擇題
| A. | a=5 | B. | a=-5 | C. | a=$\frac{1}{5}$ | D. | a=-$\frac{1}{5}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $x-\frac{1}{2}y$ | B. | $\frac{3}{7}x$ | C. | $\frac{1}{x-1}$ | D. | 0 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
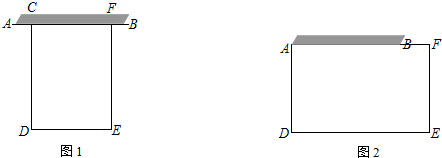
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
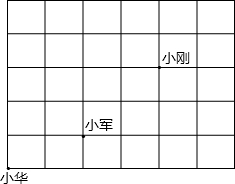 課間操時小華、小軍、小剛的位置如圖所示,小華對小剛說,如果我的位置用(0,0)表示,小軍的位置用(2,1)表示,那么小剛的位置可以用坐標表示成(4,3).
課間操時小華、小軍、小剛的位置如圖所示,小華對小剛說,如果我的位置用(0,0)表示,小軍的位置用(2,1)表示,那么小剛的位置可以用坐標表示成(4,3).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com