
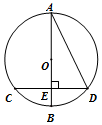
 如圖,在⊙O中,直徑AB⊥CD于點E,AB=8,BE=1.5,將$\widehat{AD}$沿著AD對折,對折之后的弧稱為M,則點O與M所在圓的位置關系為( )
如圖,在⊙O中,直徑AB⊥CD于點E,AB=8,BE=1.5,將$\widehat{AD}$沿著AD對折,對折之后的弧稱為M,則點O與M所在圓的位置關系為( )| A. | 點在圓上 | B. | 點在圓內 | C. | 點在圓外 | D. | 無法確定 |
分析 作輔助線,根據垂徑定理得:AF=FD=$\frac{1}{2}$AD,根據直徑得出半徑的長為4,根據勾股定理計算得出ED和AD的長,接著計算OF和FH的長,做比較,O與新圓心的距離小于半徑的長,得出結論.
解答 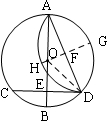 解:過O作OF⊥AD,交⊙O于G,交M于H,連接OD,
解:過O作OF⊥AD,交⊙O于G,交M于H,連接OD,
∵AB為⊙O的直徑,AB=8,
∴OA=OB=OG=OD=4,
∵BE=1.5,
∴OE=4-1.5=2.5,
在Rt△OED中,由勾股定理得:DE=$\sqrt{O{D}^{2}-O{E}^{2}}$=$\sqrt{{4}^{2}-(\frac{5}{2})^{2}}$=$\frac{\sqrt{39}}{2}$,
在RtAED中,AD=$\sqrt{A{E}^{2}+E{D}^{2}}$=$\sqrt{(\frac{13}{2})^{2}+(\frac{\sqrt{39}}{2})^{2}}$=$\sqrt{\frac{208}{4}}$=2$\sqrt{13}$,
∵OF⊥AD,
∴AF=$\frac{1}{2}$AD=$\sqrt{13}$,
由勾股定理得:OF=$\sqrt{O{A}^{2}-A{F}^{2}}$=$\sqrt{{4}^{2}-(\sqrt{13})^{2}}$=$\sqrt{3}$,
由折疊得:M所在圓與圓O是等圓,
∴M所在圓的半徑為4,
∴FH=FG=4-$\sqrt{3}$,
∵4-$\sqrt{3}$>$\sqrt{3}$,
∴FH>OF,
∴O在M所在圓內,
故選B.
點評 本題考查了點和圓的位置關系、垂徑定理、勾股定理、折疊的性質,要知道將弧沿所對的弦折疊時,所構成的圓與原來的圓是等圓,其圓心在這條弦的垂直平分線上,并熟練掌握點和圓的位置關系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{10}$是無理數 | B. | $3<\sqrt{10}<4$ | ||
| C. | 10的平方根是$\sqrt{10}$ | D. | $\sqrt{10}$是10的算術平方根 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
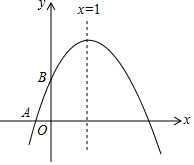 如圖,已知二次函數y=ax2+bx+c(a≠0)的圖象與x軸交于點A(-1,0),頂點坐標為(1,n),與y軸的交點在(0,2)和(0,3)之間(不包括端點).有下列結論:①當x>3時,y<0;②n=c-a;③3a+b>0;④-1<a<-$\frac{2}{3}$.其中正確的結論有( )
如圖,已知二次函數y=ax2+bx+c(a≠0)的圖象與x軸交于點A(-1,0),頂點坐標為(1,n),與y軸的交點在(0,2)和(0,3)之間(不包括端點).有下列結論:①當x>3時,y<0;②n=c-a;③3a+b>0;④-1<a<-$\frac{2}{3}$.其中正確的結論有( )| A. | 1 個 | B. | 2 個 | C. | 3 個 | D. | 4 個 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com